4NF Decomposition for Conflict-Free Dependency Sets: Difference between revisions
Jump to navigation
Jump to search
(Created page with "{{DISPLAYTITLE:4NF Decomposition for Conflict-Free Dependency Sets (4NF Decomposition)}} == Description == 4NF Decomposition is the problem of decomposing a relation schema into fourth normal form (4NF). This variation specifies that the input dependency set is conflict-free. A relation schema $R^*$ is in fourth normal form (4NF) if, whenever a nontrivial multivalued dependency $X \rightarrow \rightarrow Y$ holds for $R^*$, then so does the functiunal dependency $X \r...") |
No edit summary |
||
| Line 46: | Line 46: | ||
|} | |} | ||
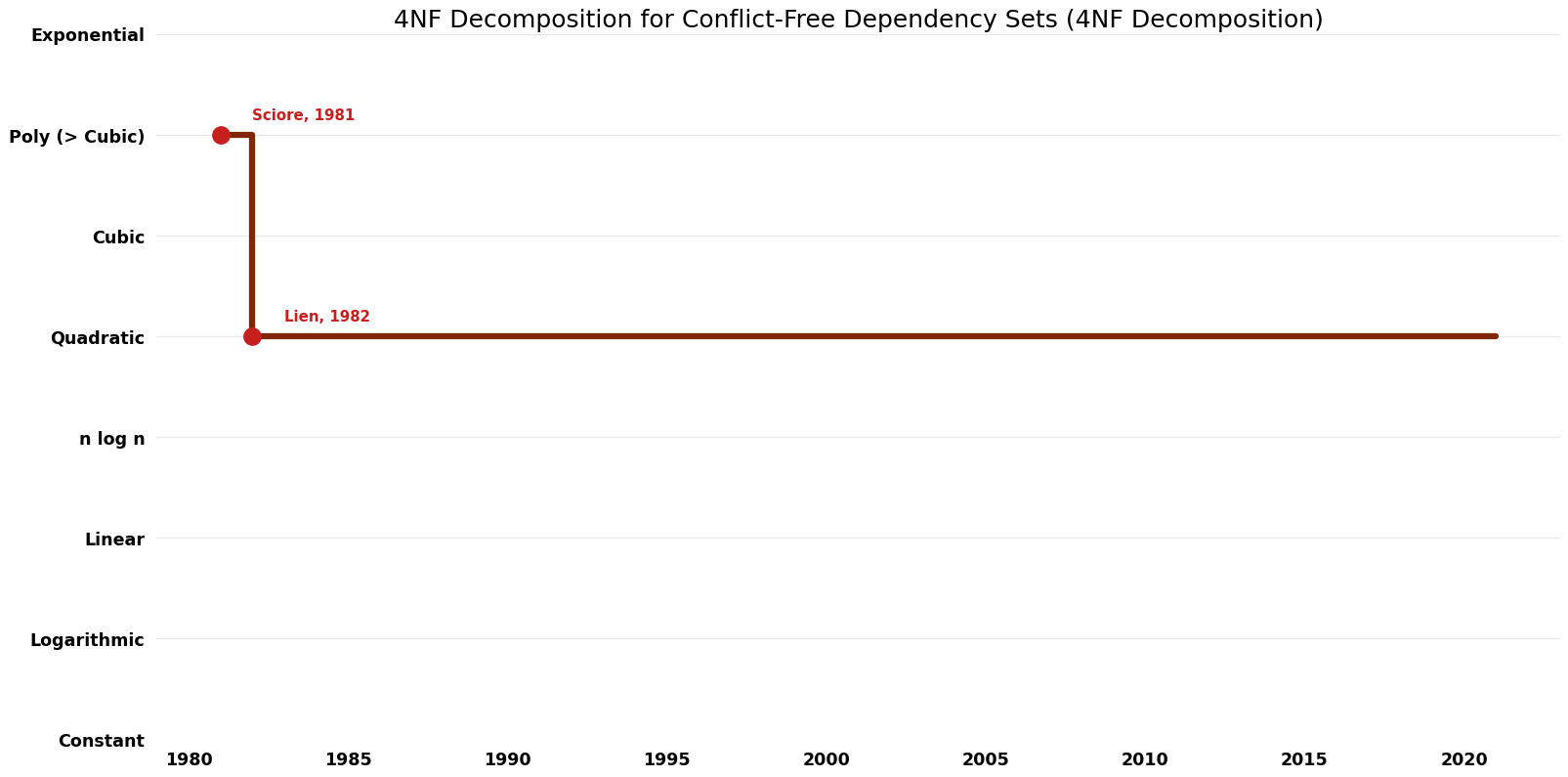
== Time Complexity | == Time Complexity Graph == | ||
[[File:4NF Decomposition - 4NF Decomposition for Conflict-Free Dependency Sets - Time.png|1000px]] | [[File:4NF Decomposition - 4NF Decomposition for Conflict-Free Dependency Sets - Time.png|1000px]] | ||
== Space Complexity | == Space Complexity Graph == | ||
[[File:4NF Decomposition - 4NF Decomposition for Conflict-Free Dependency Sets - Space.png|1000px]] | [[File:4NF Decomposition - 4NF Decomposition for Conflict-Free Dependency Sets - Space.png|1000px]] | ||
== Pareto | == Pareto Frontier Improvements Graph == | ||
[[File:4NF Decomposition - 4NF Decomposition for Conflict-Free Dependency Sets - Pareto Frontier.png|1000px]] | [[File:4NF Decomposition - 4NF Decomposition for Conflict-Free Dependency Sets - Pareto Frontier.png|1000px]] | ||
Revision as of 13:04, 15 February 2023
Description
4NF Decomposition is the problem of decomposing a relation schema into fourth normal form (4NF). This variation specifies that the input dependency set is conflict-free.
A relation schema $R^*$ is in fourth normal form (4NF) if, whenever a nontrivial multivalued dependency $X \rightarrow \rightarrow Y$ holds for $R^*$, then so does the functiunal dependency $X \rightarrow A$ for every column name $A$ of $R^*$. Intuitively all dependencies are the result of keys. In particular a 4NF relation schema can have no nontrivial multivalued dependencies that are not functional dependencies.
Related Problems
Generalizations: 4NF Decomposition
Related: 4NF Decomposition for Functional and Multivalued Dependency Sets
Parameters
No parameters found.
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Tradu; Mirc | 1967 | $O({2}^n)$ | Exact | Deterministic | ||
| Xu; Renio | 1972 | $O({2}^n)$ | Exact | Deterministic | ||
| Derek's Algorithm | 1983 | $O({2}^n)$ | Exact | Deterministic | ||
| Russell et. al. | 1989 | $O({2}^n)$ | Exact | Deterministic | ||
| Maxwell | 2000 | $O({2}^n)$ | Exact | Deterministic | ||
| Derek's + Maxwell | 2001 | $O({2}^n)$ | Exact | Deterministic | ||
| Naive | 1956 | $O({2}^n)$ | Exact | Deterministic | ||
| Trino | 2004 | $O({2}^n)$ | Exact | Deterministic | ||
| Lien | 1982 | $O(k^{2} n^{2})$ | $O(k^{2})$ | Exact | Deterministic | Time |
| Sciore | 1981 | poly-time | Exact | Deterministic | Time |
Time Complexity Graph
Space Complexity Graph
Pareto Frontier Improvements Graph
