Determinant of Matrices with Integer Entries: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 6: | Line 6: | ||
== Parameters == | == Parameters == | ||
n: dimension of matrix | $n$: dimension of matrix | ||
== Table of Algorithms == | == Table of Algorithms == | ||
| Line 16: | Line 16: | ||
|- | |- | ||
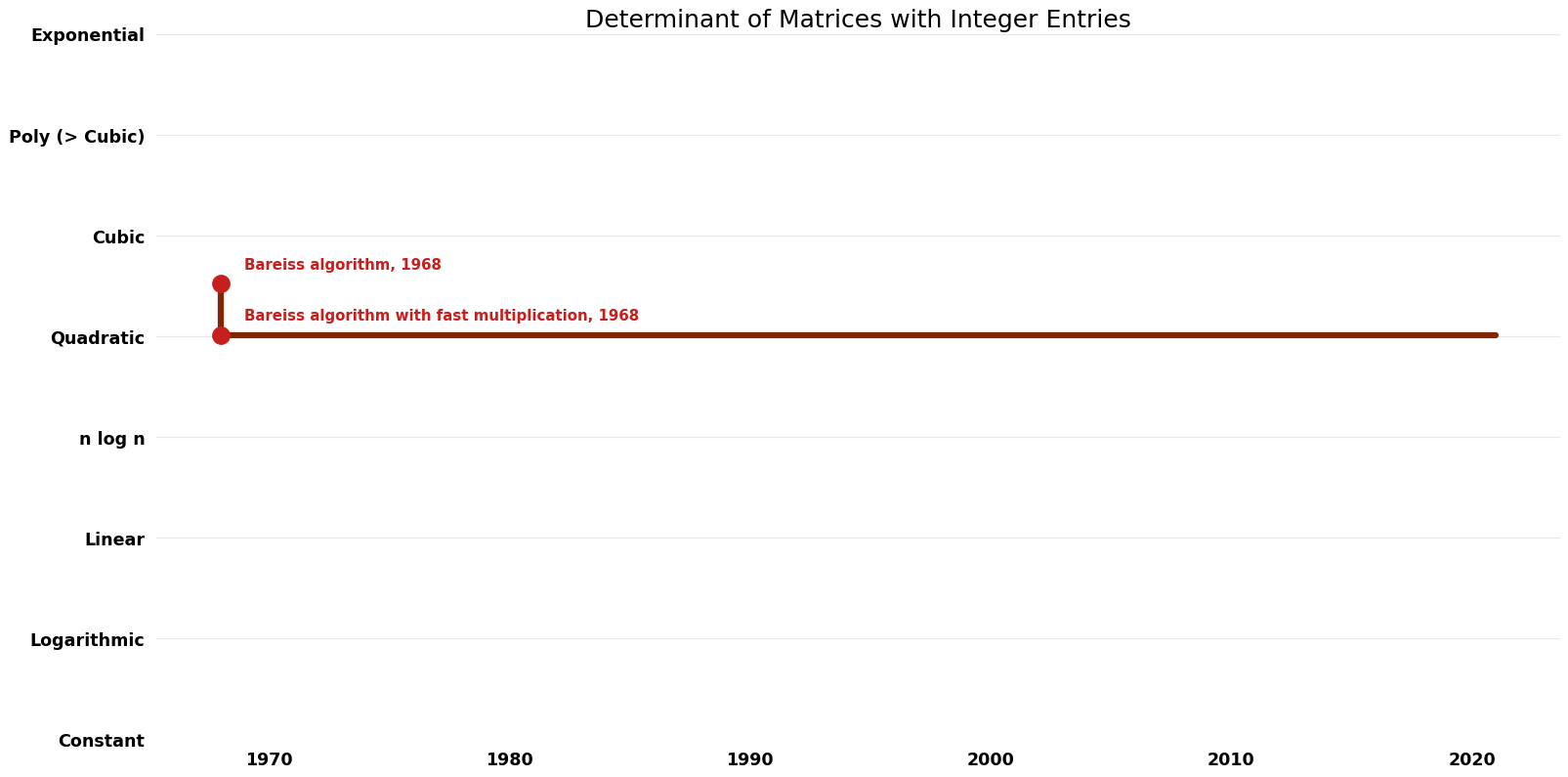
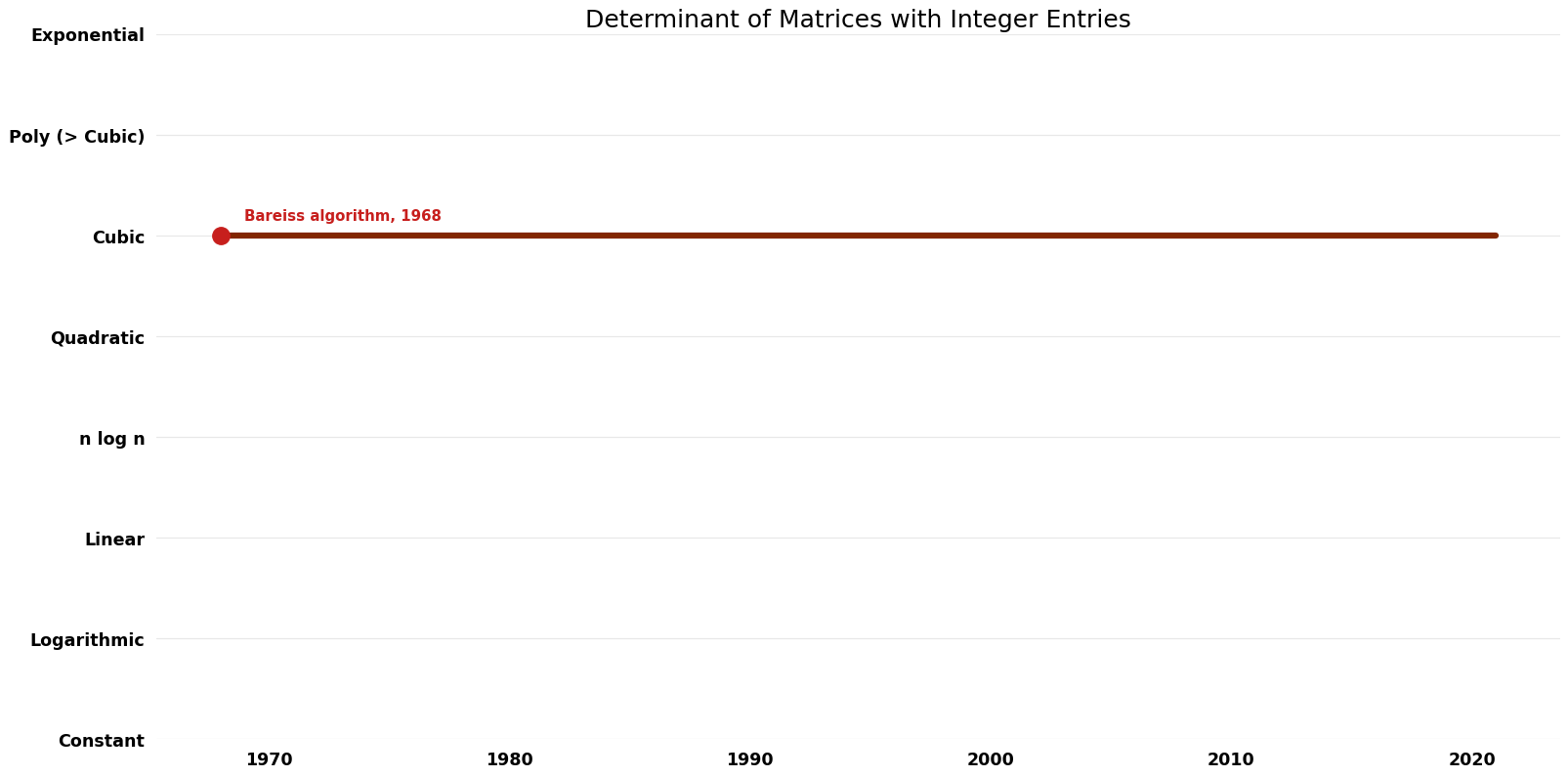
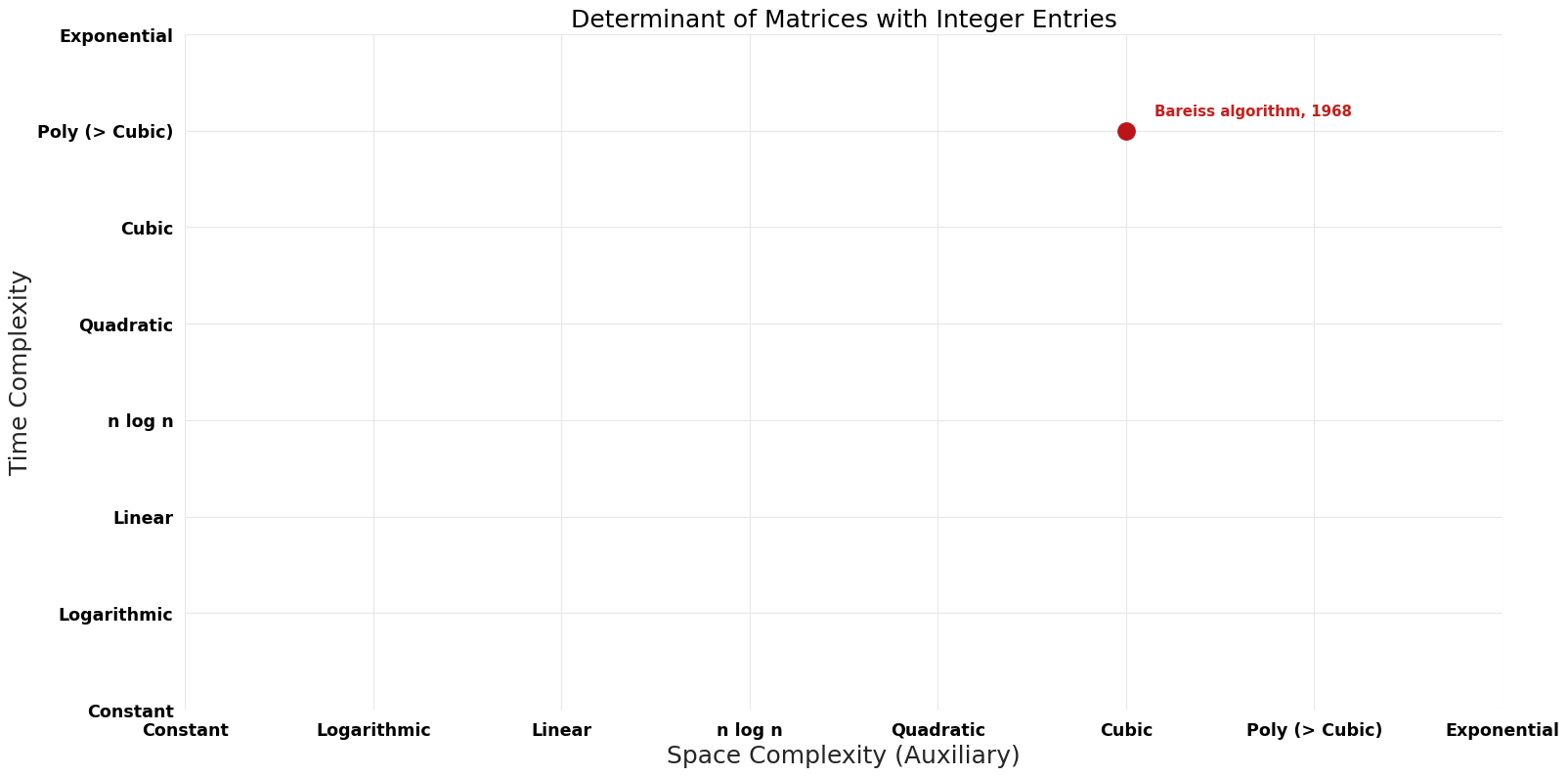
| [[Bareiss algorithm (Determinant of Matrices with Integer Entries Determinant of Matrices with Integer Entries)|Bareiss algorithm]] || 1968 || $O(n^{5}L^{2} (log(n)$^{2} + L^{2})) || $O(n^{2}(n*log(n)$+nL)) || Exact || Deterministic || [https://www.ams.org/journals/mcom/1968-22-103/S0025-5718-1968-0226829-0/S0025-5718-1968-0226829-0.pdf Time] | | [[Bareiss algorithm (Determinant of Matrices with Integer Entries Determinant of Matrices with Integer Entries)|Bareiss algorithm]] || 1968 || $O(n^{5} L^{2} (\log(n)$^{2} + L^{2})) || $O(n^{2}(n*log(n)$+nL)) || Exact || Deterministic || [https://www.ams.org/journals/mcom/1968-22-103/S0025-5718-1968-0226829-0/S0025-5718-1968-0226829-0.pdf Time] | ||
|- | |- | ||
| [[Bareiss algorithm with fast multiplication (Determinant of Matrices with Integer Entries Determinant of Matrices with Integer Entries)|Bareiss algorithm with fast multiplication]] || 1968 || $O(n^{4}L(log(n)$ + L)log(log(n) + L)) || $O(n^{2}(n*log(n)$+nL)) || Exact || Deterministic || | | [[Bareiss algorithm with fast multiplication (Determinant of Matrices with Integer Entries Determinant of Matrices with Integer Entries)|Bareiss algorithm with fast multiplication]] || 1968 || $O(n^{4} L (\log(n)$ + L) \log(\log(n) + L)) || $O(n^{2}(n*log(n)$+nL)) || Exact || Deterministic || | ||
|- | |- | ||
|} | |} | ||
Revision as of 09:24, 10 April 2023
Description
Calculate the determinant of a given matrix with integer matrices. For such matrices, the determinant is also an integer.
Parameters
$n$: dimension of matrix
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Bareiss algorithm | 1968 | $O(n^{5} L^{2} (\log(n)$^{2} + L^{2})) | $O(n^{2}(n*log(n)$+nL)) | Exact | Deterministic | Time |
| Bareiss algorithm with fast multiplication | 1968 | $O(n^{4} L (\log(n)$ + L) \log(\log(n) + L)) | $O(n^{2}(n*log(n)$+nL)) | Exact | Deterministic |