Tower of Hanoi: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 6: | Line 6: | ||
== Parameters == | == Parameters == | ||
n: number of discs | $n$: number of discs | ||
p: number of pegs | $p$: number of pegs | ||
== Table of Algorithms == | == Table of Algorithms == | ||
| Line 18: | Line 18: | ||
|- | |- | ||
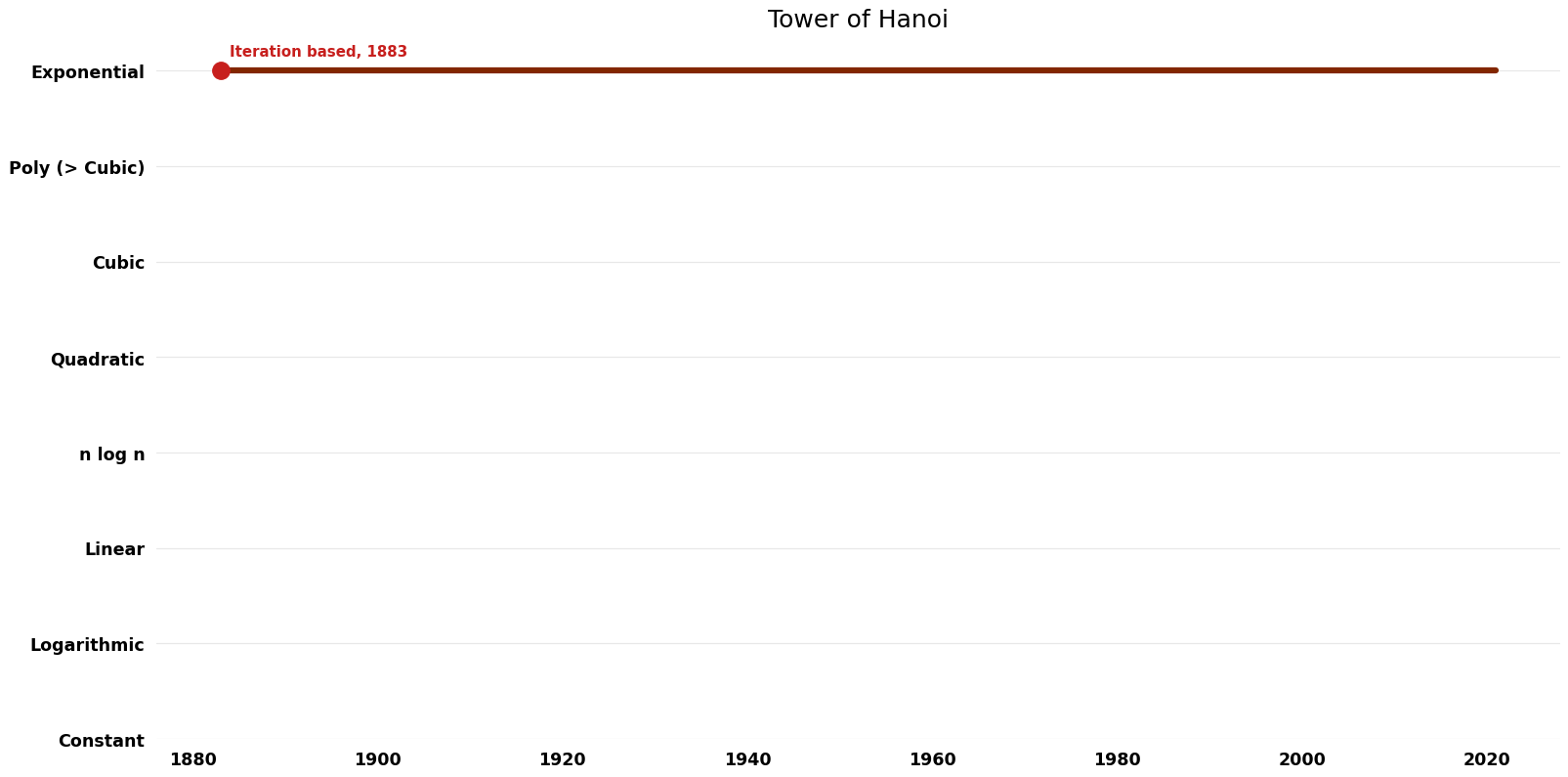
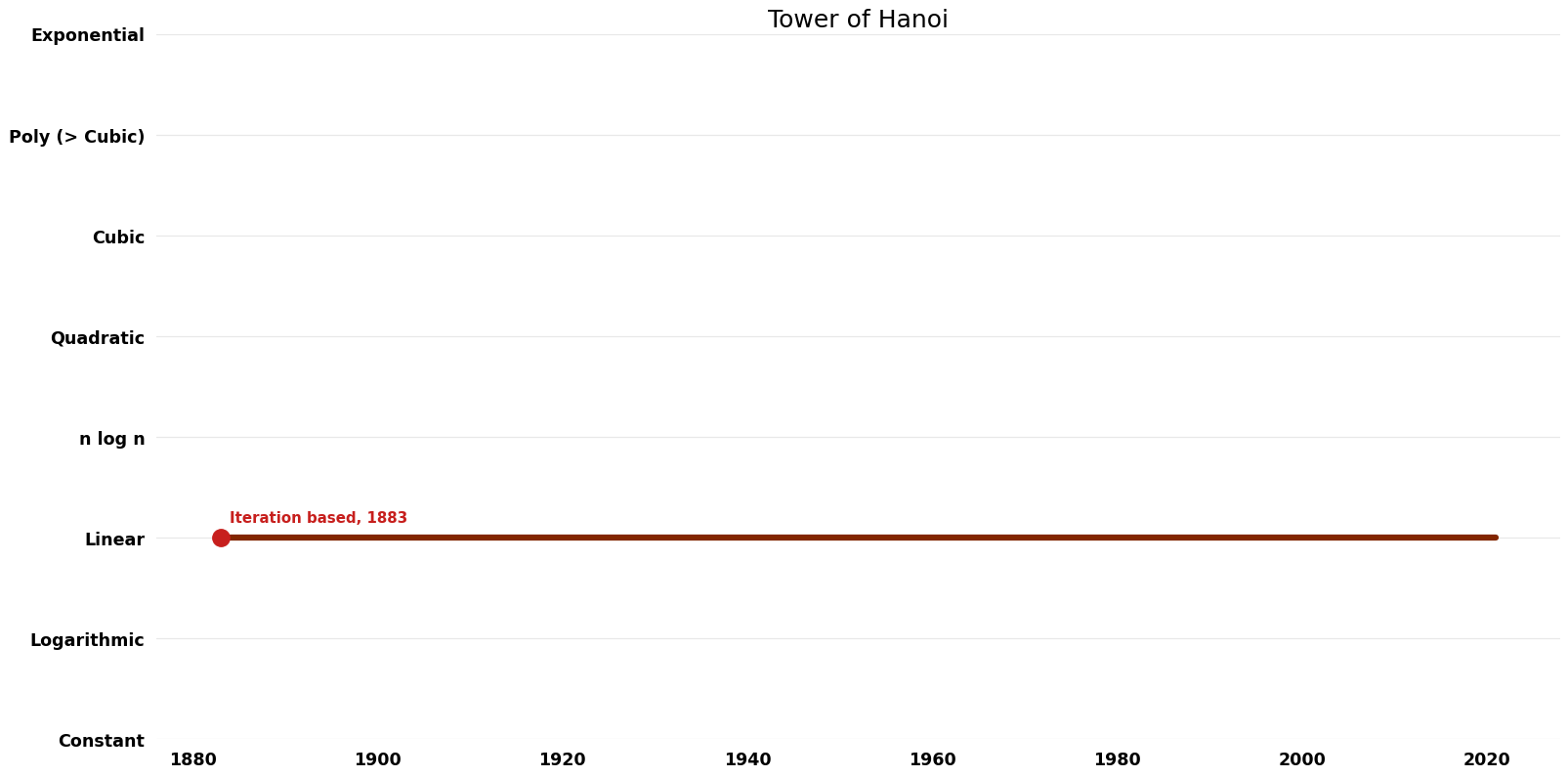
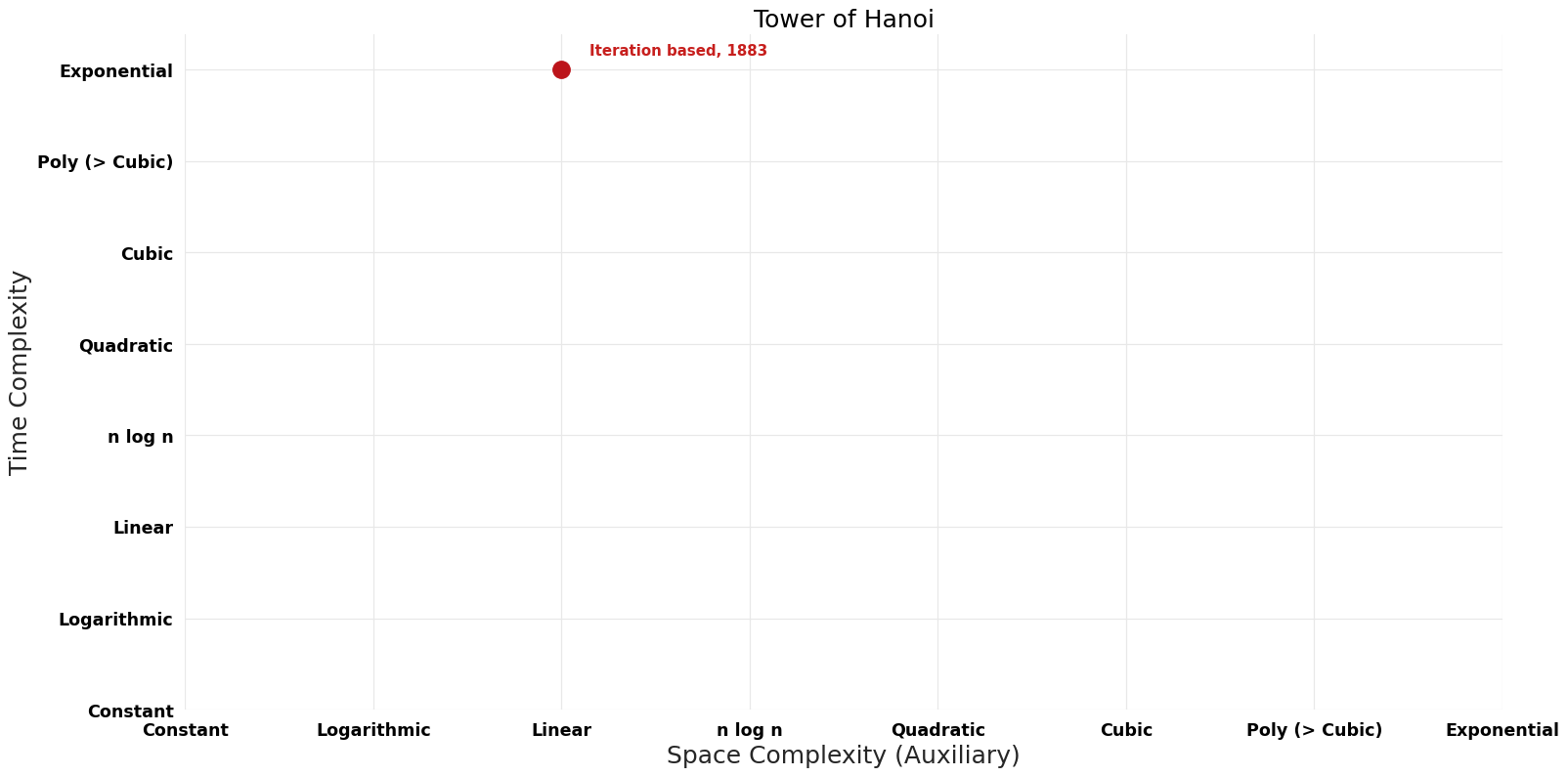
| [[Iteration based (Tower of Hanoi Tower of Hanoi)|Iteration based]] || 1883 || $O({2}^n)$ || $O(n)$ | | [[Iteration based (Tower of Hanoi Tower of Hanoi)|Iteration based]] || 1883 || $O({2}^n)$ || $O(n)$ || Exact || Deterministic || | ||
|- | |- | ||
| [[Recursion based (Tower of Hanoi Tower of Hanoi)|Recursion based]] || 1940 || $O({2}^n)$ || $O(n | | [[Recursion based (Tower of Hanoi Tower of Hanoi)|Recursion based]] || 1940 || $O({2}^n)$ || $O(n \log n)$ || Exact || Deterministic || | ||
|- | |- | ||
| [[Non-recursion based (Tower of Hanoi Tower of Hanoi)|Non-recursion based]] || 1940 || $O({2}^n)$ || $O(n)$ | | [[Non-recursion based (Tower of Hanoi Tower of Hanoi)|Non-recursion based]] || 1940 || $O({2}^n)$ || $O(n)$ || Exact || Deterministic || | ||
|- | |- | ||
| [[Gray-code based (Tower of Hanoi Tower of Hanoi)|Gray-code based]] || 1940 || $O({2}^n)$ || $O(n)$ | | [[Gray-code based (Tower of Hanoi Tower of Hanoi)|Gray-code based]] || 1940 || $O({2}^n)$ || $O(n)$ || Exact || Deterministic || | ||
|- | |- | ||
| [[Hanoi graph (Tower of Hanoi Tower of Hanoi)|Hanoi graph]] || 2008 || $O({2}^n)$ || || Exact || Deterministic || [https://books.google.com/books/about/Topics_in_Graph_Theory.html?id=pSv3XotPCQgC Time] | | [[Hanoi graph (Tower of Hanoi Tower of Hanoi)|Hanoi graph]] || 2008 || $O({2}^n)$ || || Exact || Deterministic || [https://books.google.com/books/about/Topics_in_Graph_Theory.html?id=pSv3XotPCQgC Time] | ||
Revision as of 08:25, 10 April 2023
Description
The Tower of Hanoi puzzle consists of $n$ discs, no two of the same size, stacked on $p \geq 3$ vertical pegs, in such a way that no disc lies on top of a smaller disc. A permissible $move$ is to take the top disc from one of the pegs and move it to one of the other pegs, as long as it is not placed on top of a smaller disc. Initially, they are all stacked on the first peg. The goal is to end up with them all stacked on the last peg.
Parameters
$n$: number of discs
$p$: number of pegs
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Iteration based | 1883 | $O({2}^n)$ | $O(n)$ | Exact | Deterministic | |
| Recursion based | 1940 | $O({2}^n)$ | $O(n \log n)$ | Exact | Deterministic | |
| Non-recursion based | 1940 | $O({2}^n)$ | $O(n)$ | Exact | Deterministic | |
| Gray-code based | 1940 | $O({2}^n)$ | $O(n)$ | Exact | Deterministic | |
| Hanoi graph | 2008 | $O({2}^n)$ | Exact | Deterministic | Time |
Time Complexity Graph
Error creating thumbnail: Unable to save thumbnail to destination
Space Complexity Graph
Error creating thumbnail: Unable to save thumbnail to destination
Time-Space Tradeoff
Error creating thumbnail: Unable to save thumbnail to destination