Motif Search: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 61: | Line 61: | ||
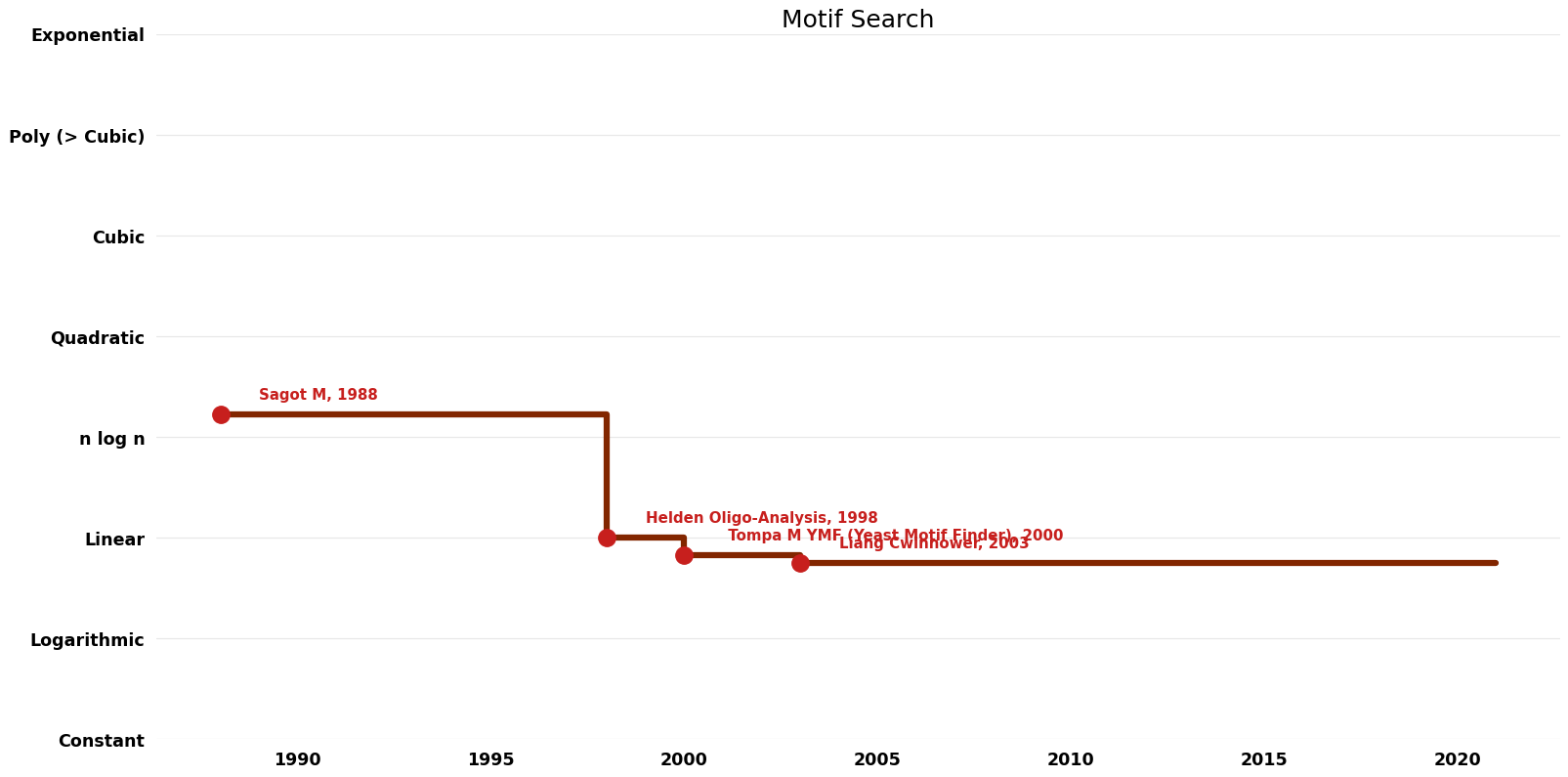
[[File:Motif Search - Time.png|1000px]] | [[File:Motif Search - Time.png|1000px]] | ||
Latest revision as of 09:11, 28 April 2023
Description
Motif search is the problem of identifying motifs, recurring or conserved patterns, in the strings (typically biological sequence data sets).
Parameters
$n$: size of set of input strings
$m$: size of input strings
$k$: length of substrings
$\sigma$: function $V(k, m)$ defined as the number of $k$-mers that are at most $m$ Hamming distance from the motif space
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Lawrence, Reilly | 1990 | $O(nm)$ | $O(nm)$ | Deterministic | Time & Space | |
| Lawrence Gibbs Sampling | 1993 | $O(nm)$ | $O(n + m)$ | Deterministic | Time | |
| MotifSampler | 2001 | $O(nm)$ | $O(n + m)$ | Deterministic | Time | |
| Speller | 1998 | $O(mn^{2} \sigma)$ | $O(mn^{2}/w)$ | Exact | Deterministic | Time & Space |
| Mitra | 2002 | $O(k nm \sigma)$ | $O(mnk)$ | Exact | Deterministic | Time & Space |
| Census | 2003 | $O(k nm \sigma)$ | $O(mnk)$ | Exact | Deterministic | Time & Space |
| Risotto | 2006 | $O(mn^{2} \sigma)$ | $O(mn^{2})$ | Exact | Deterministic | Time & Space |
| PMS | 2007 | $O(nm^{2} \sigma)$ | $O(m^{2} n)$ | Exact | Deterministic | Time & Space |
| Roth AlignACE | 1998 | $O(nm)$ | $O(n + m)$ | Deterministic | Time | |
| Helden Oligo-Analysis | 1998 | $O(mn)$ | $O(m)$ | Exact | Deterministic | Time |
| van Helden J; Rios AF; Collado-Vides J | 2000 | $O(mn)$ | $O(m)$ | Exact | Deterministic | Time |
| Tompa M | 1999 | $O(mn)$ | $O(m^{2})$ | Exact | Deterministic | Time |
| Sinha S; Tompa M YMF (Yeast Motif Finder) | 2000 | $O(n^{0.{6}6} m)$ | $O(m)$ | Exact | Deterministic | Time |
| Bailey TL; Elkan C MEME | 1995 | $O(n^{2}m^{2})$ | $O(mn)$ | Exact | Deterministic | Time |
| Sagot M | 1988 | $O(n \log(n)$ m^{1.{4}5}) | $O(mn^{2}/w)$ | Exact | Deterministic | Time & Space |
| Liang Cwinnower | 2003 | $O(nm^{0.5})$ | $O(m^{2})$ | Exact | Deterministic | Time |
| Kingsford | 2006 | $O(mn)$ | $O(m^{2}n^{2})$ | Exact | Deterministic | Time |