Alphabetic Tree Problem: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 30: | Line 30: | ||
|} | |} | ||
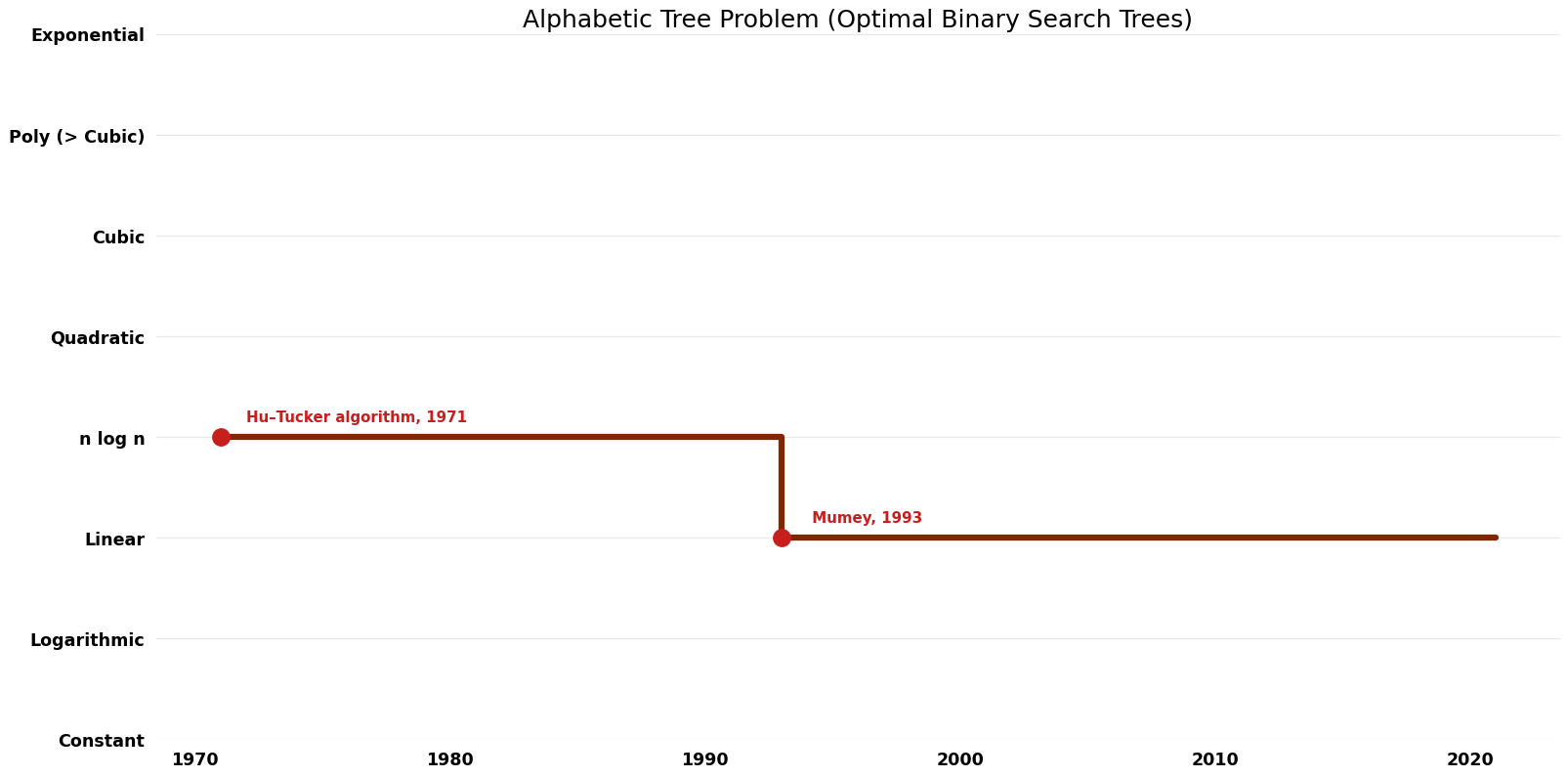
== Time Complexity | == Time Complexity Graph == | ||
[[File:Optimal Binary Search Trees - Alphabetic Tree Problem - Time.png|1000px]] | [[File:Optimal Binary Search Trees - Alphabetic Tree Problem - Time.png|1000px]] | ||
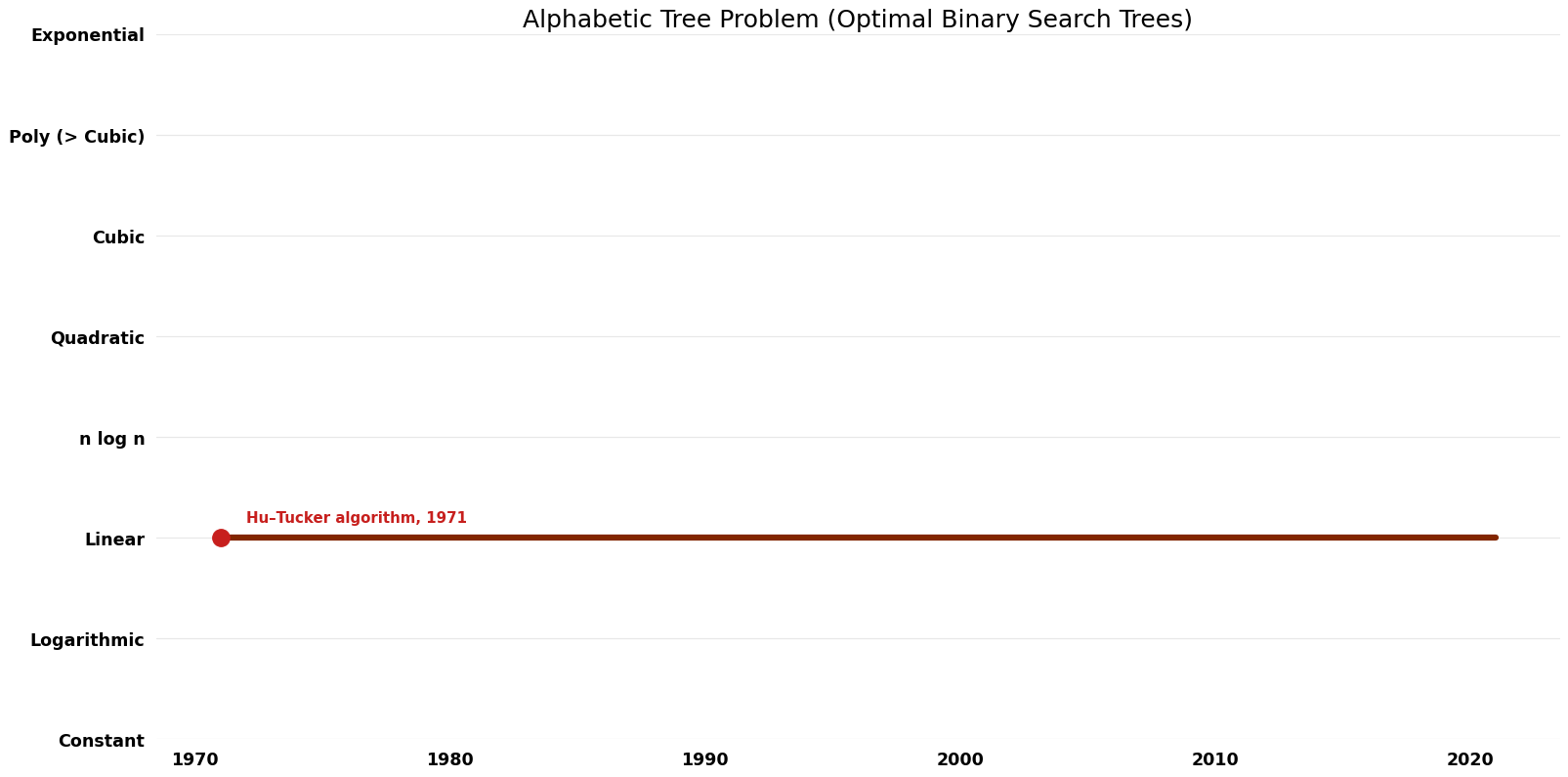
== Space Complexity | == Space Complexity Graph == | ||
[[File:Optimal Binary Search Trees - Alphabetic Tree Problem - Space.png|1000px]] | [[File:Optimal Binary Search Trees - Alphabetic Tree Problem - Space.png|1000px]] | ||
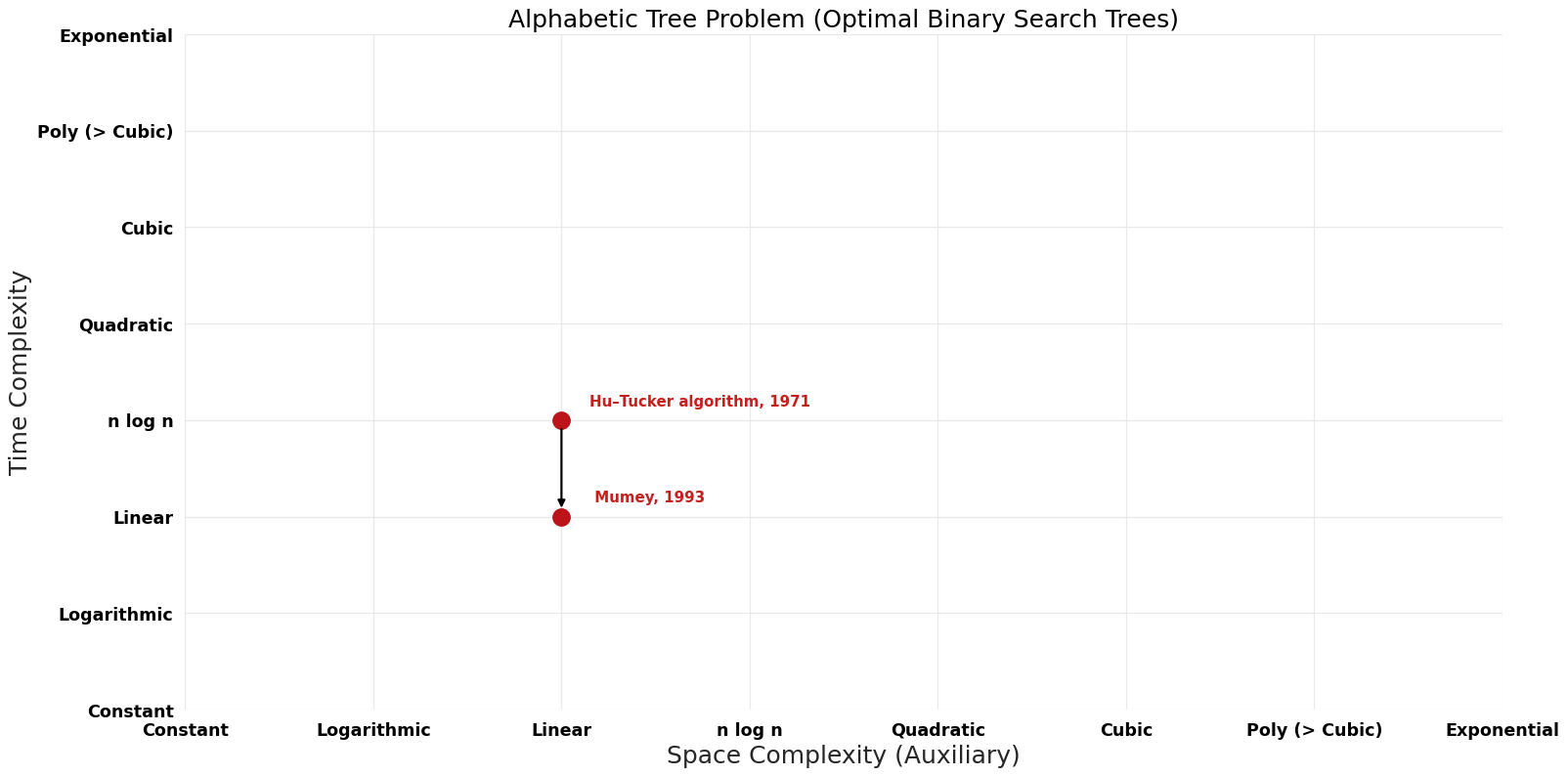
== Pareto | == Pareto Frontier Improvements Graph == | ||
[[File:Optimal Binary Search Trees - Alphabetic Tree Problem - Pareto Frontier.png|1000px]] | [[File:Optimal Binary Search Trees - Alphabetic Tree Problem - Pareto Frontier.png|1000px]] | ||
Revision as of 13:04, 15 February 2023
Description
A variant of the OBST problem is when only the gaps have nonzero access probabilities, and is called the optimal alphabetic tree problem.
Related Problems
Generalizations: Optimal Binary Search Tree Problem
Related: Approximate OBST, Huffman Encoding
Parameters
n: number of elements
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Klawe; Mumey | 1993 | $O(n)$ | $O(n)$ | Exact | Deterministic | Time |
| Garsia–Wachs algorithm | 1977 | $O(n \log n)$ | $O(n)$ | Exact | Deterministic | Time & Space |
| Hu–Tucker algorithm | 1971 | $O(n \log n)$ | $O(n)$ | Exact | Deterministic | Time & Space |
Time Complexity Graph
Space Complexity Graph
Pareto Frontier Improvements Graph
