Eigenpair closest to mu: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 40: | Line 40: | ||
[[File:Eigenvalues (Iterative Methods) - Eigenpair closest to mu - Space.png|1000px]] | [[File:Eigenvalues (Iterative Methods) - Eigenpair closest to mu - Space.png|1000px]] | ||
== Space | == Time-Space Tradeoff == | ||
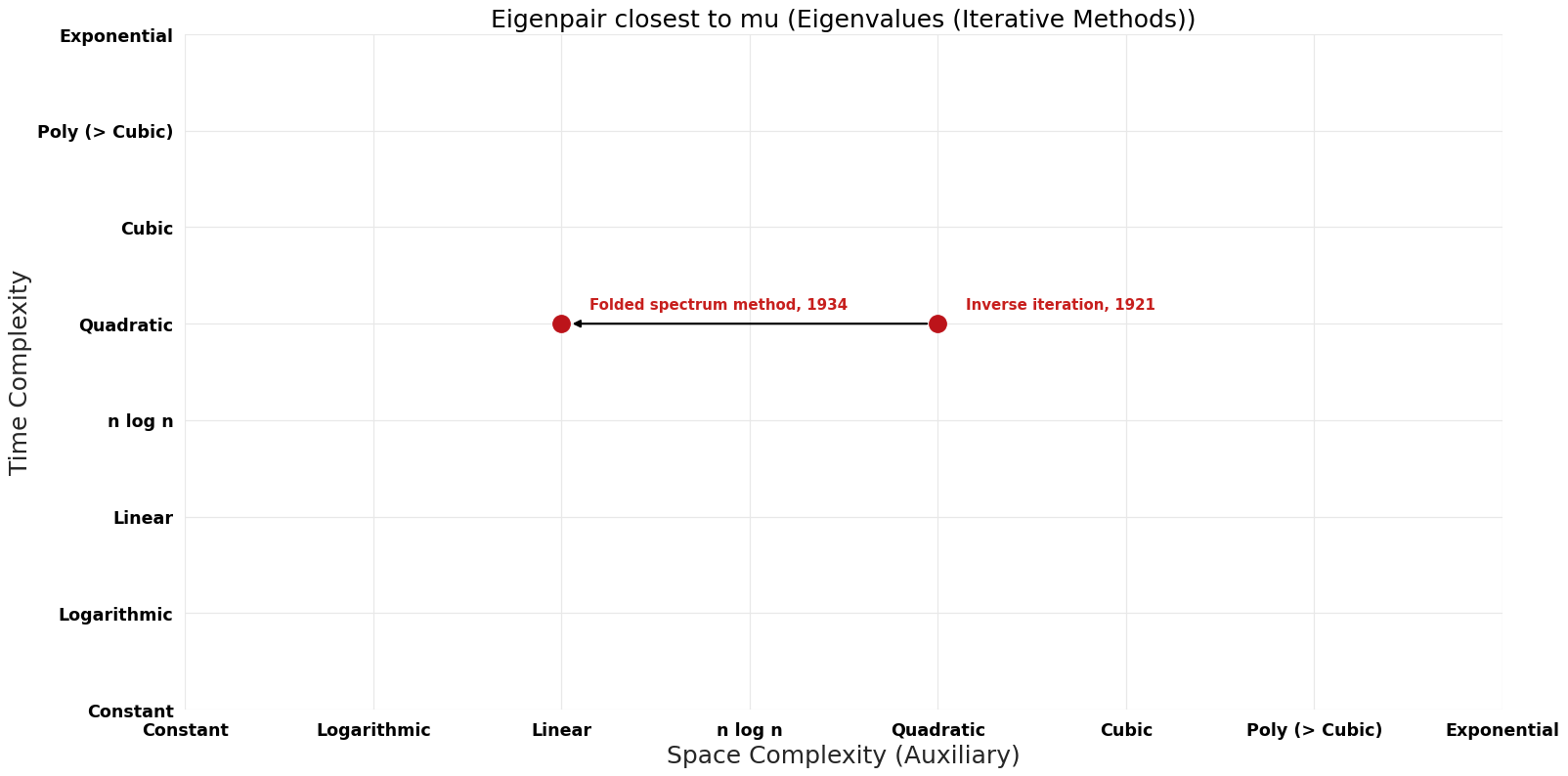
[[File:Eigenvalues (Iterative Methods) - Eigenpair closest to mu - Pareto Frontier.png|1000px]] | [[File:Eigenvalues (Iterative Methods) - Eigenpair closest to mu - Pareto Frontier.png|1000px]] | ||
Revision as of 14:45, 15 February 2023
Description
Given an $n \times n$ matrix $A$, find the eigenpair (eigenvalue and associated eigenvector) of $A$ with the eigenvalue closest to $\mu$.
Related Problems
Generalizations: Any Eigenpair
Related: All Eigenvalues, Any Eigenvalue, All Eigenpairs, Eigenpair with the Largest Eigenvalue
Parameters
No parameters found.
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
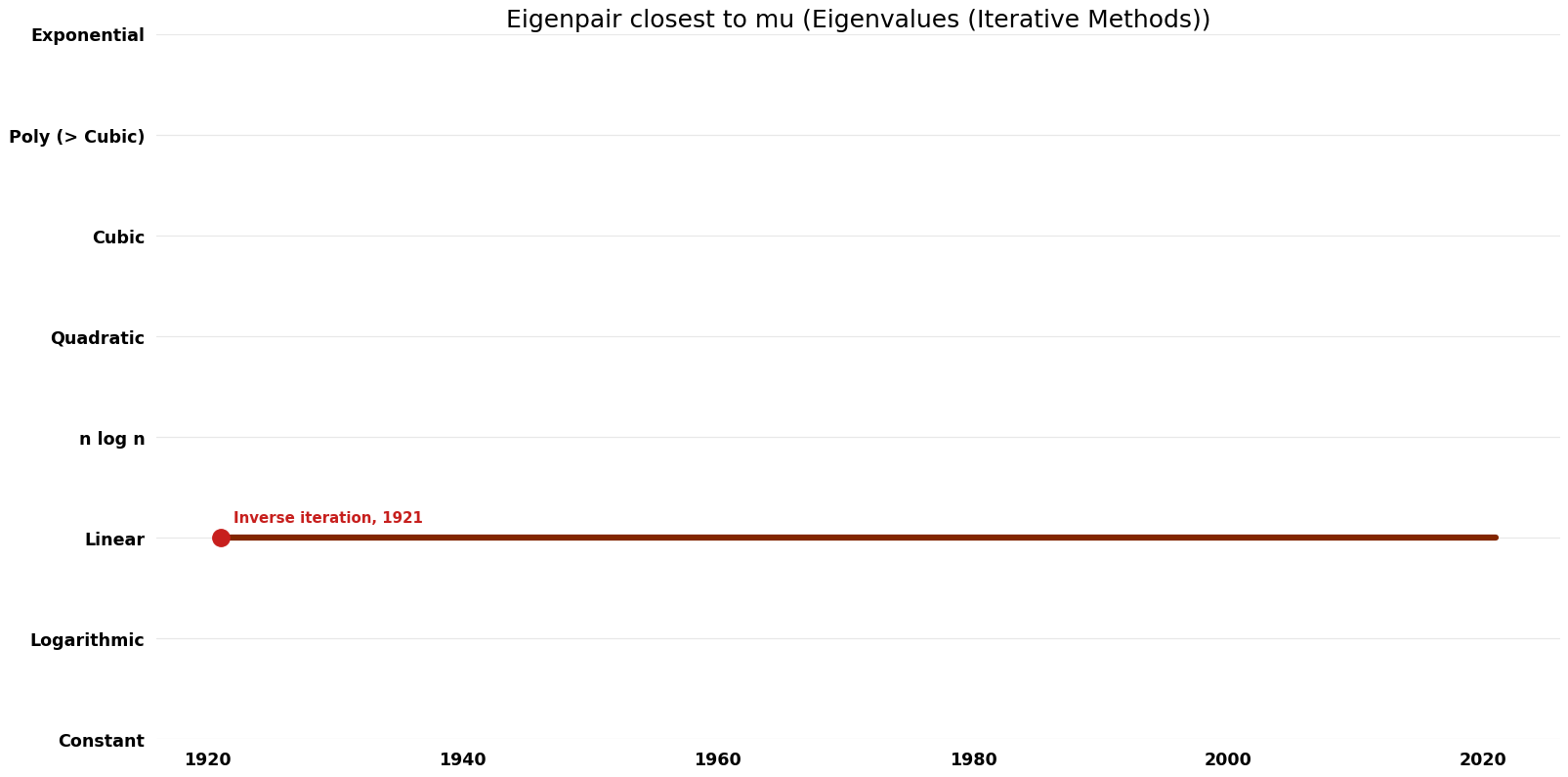
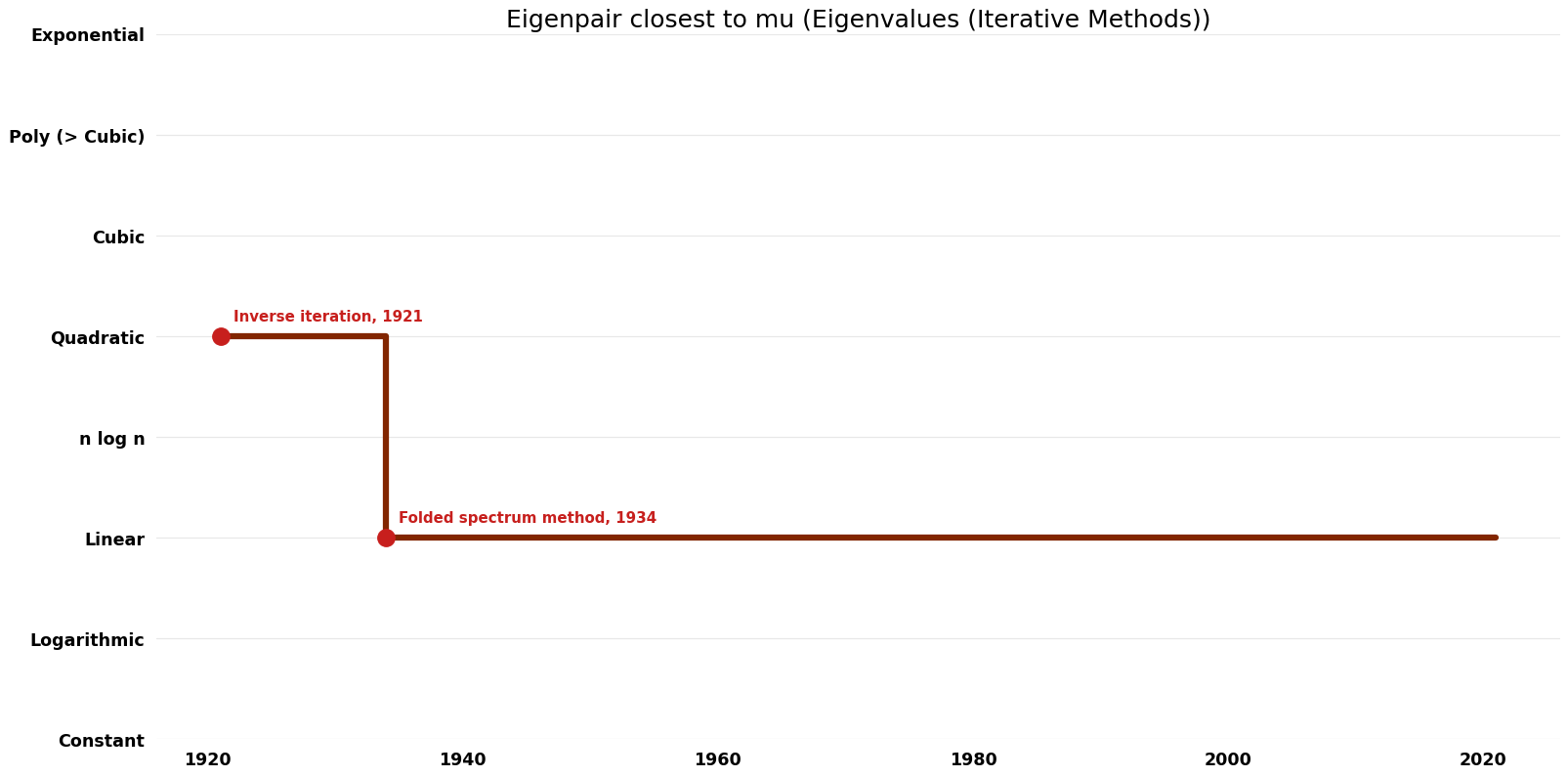
| Inverse iteration | 1921 | $O(n^{2})$ | $O(n^{2})$ | Exact | Deterministic | Time |
| LOBPCG algorithm | 1948 | $O(n^{2})$ | $O(n)$? | Exact | Deterministic | |
| Homotopy method | 1992 | $O(n^{2})$ | $O(n^{2})$?? | Exact | Deterministic | Time |
| Folded spectrum method | 1934 | $O(n^{2})$ | $O(n)$? | Exact | Deterministic | Time |
Time Complexity Graph
_-_Eigenpair_closest_to_mu_-_Time.png)
Space Complexity Graph
_-_Eigenpair_closest_to_mu_-_Space.png)
Time-Space Tradeoff
_-_Eigenpair_closest_to_mu_-_Pareto_Frontier.png)