Self-Balancing Trees Creation: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 6: | Line 6: | ||
== Parameters == | == Parameters == | ||
n: size of tree | $n$: size of tree | ||
== Table of Algorithms == | == Table of Algorithms == | ||
| Line 16: | Line 16: | ||
|- | |- | ||
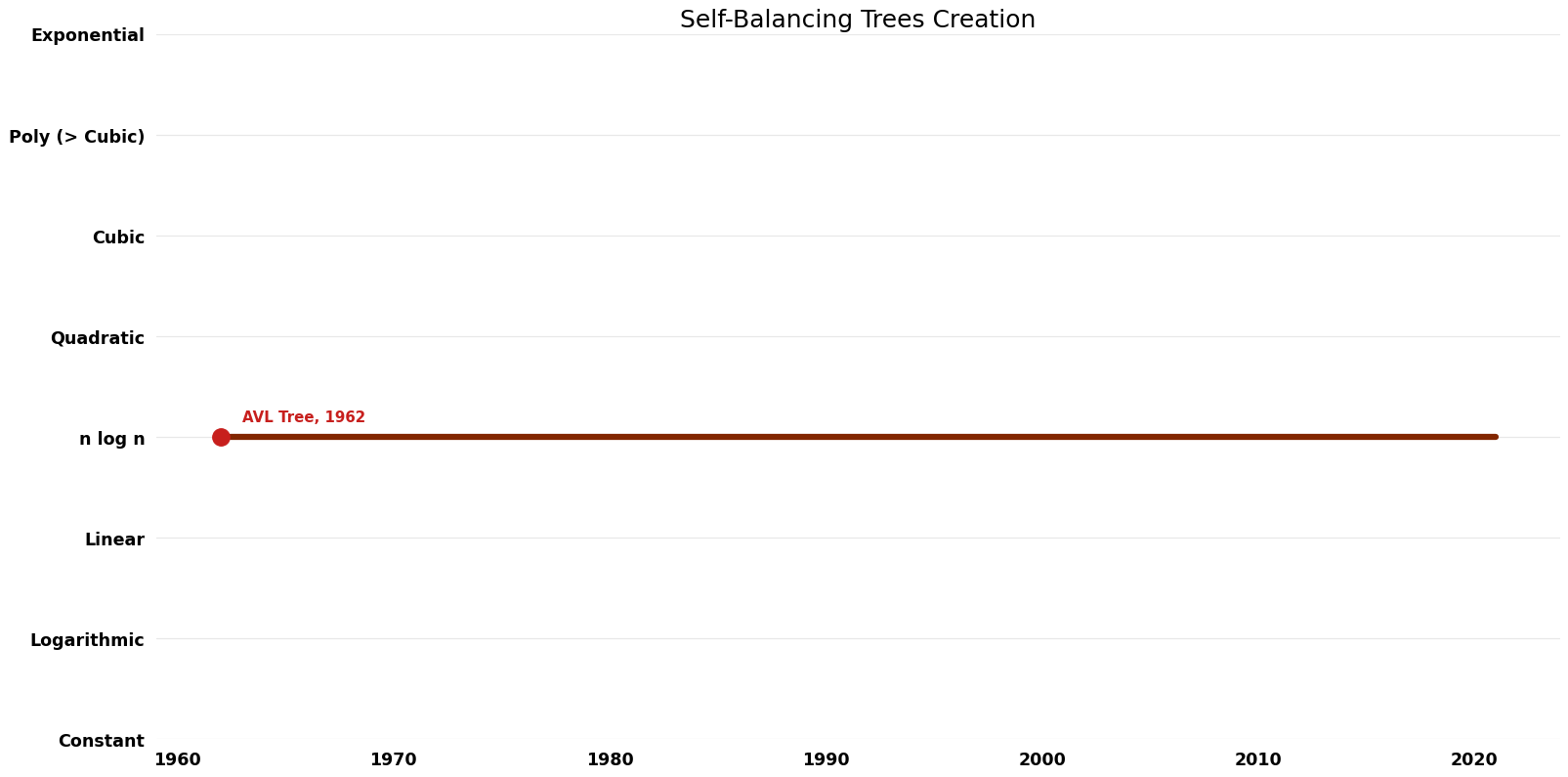
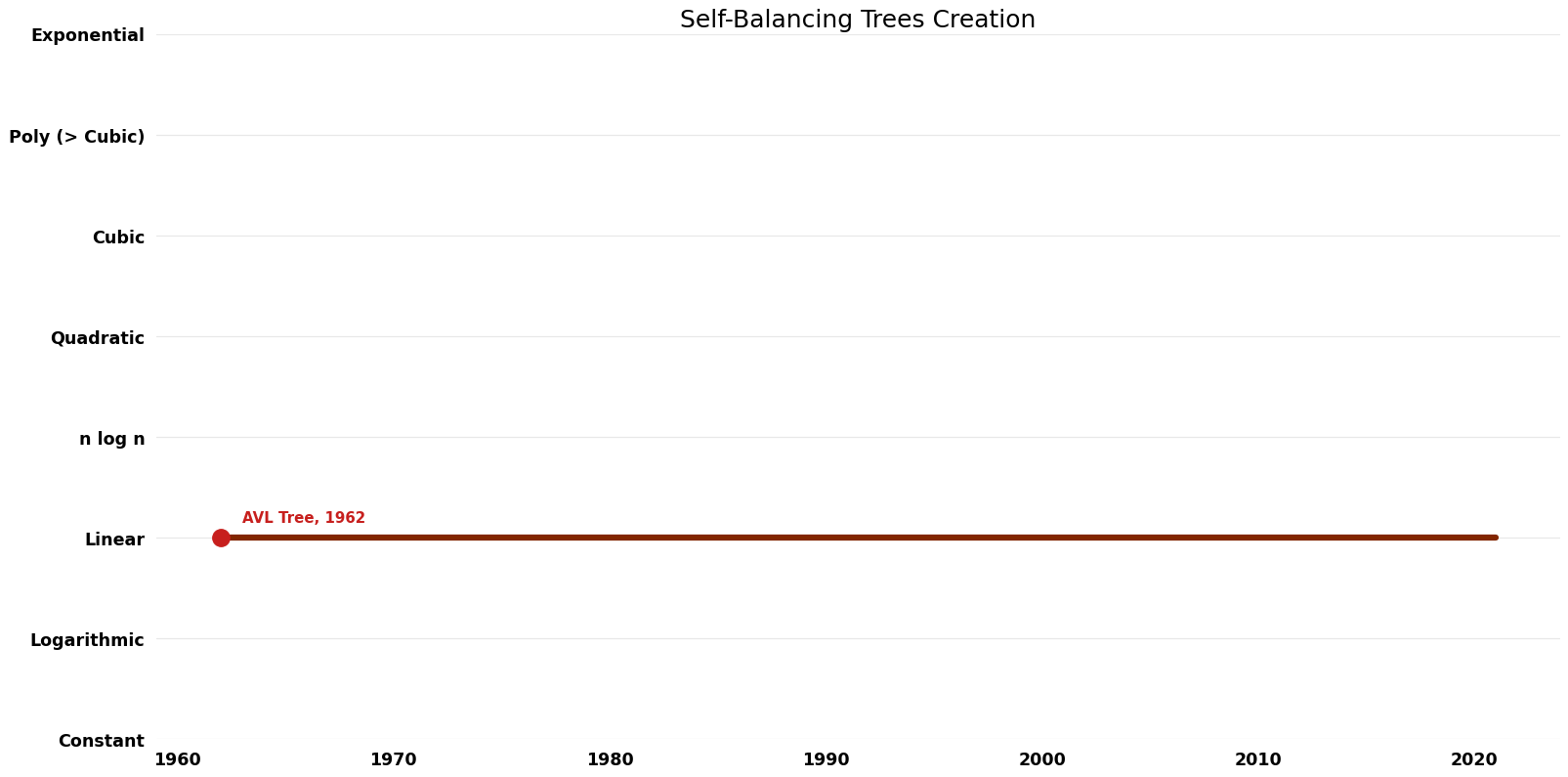
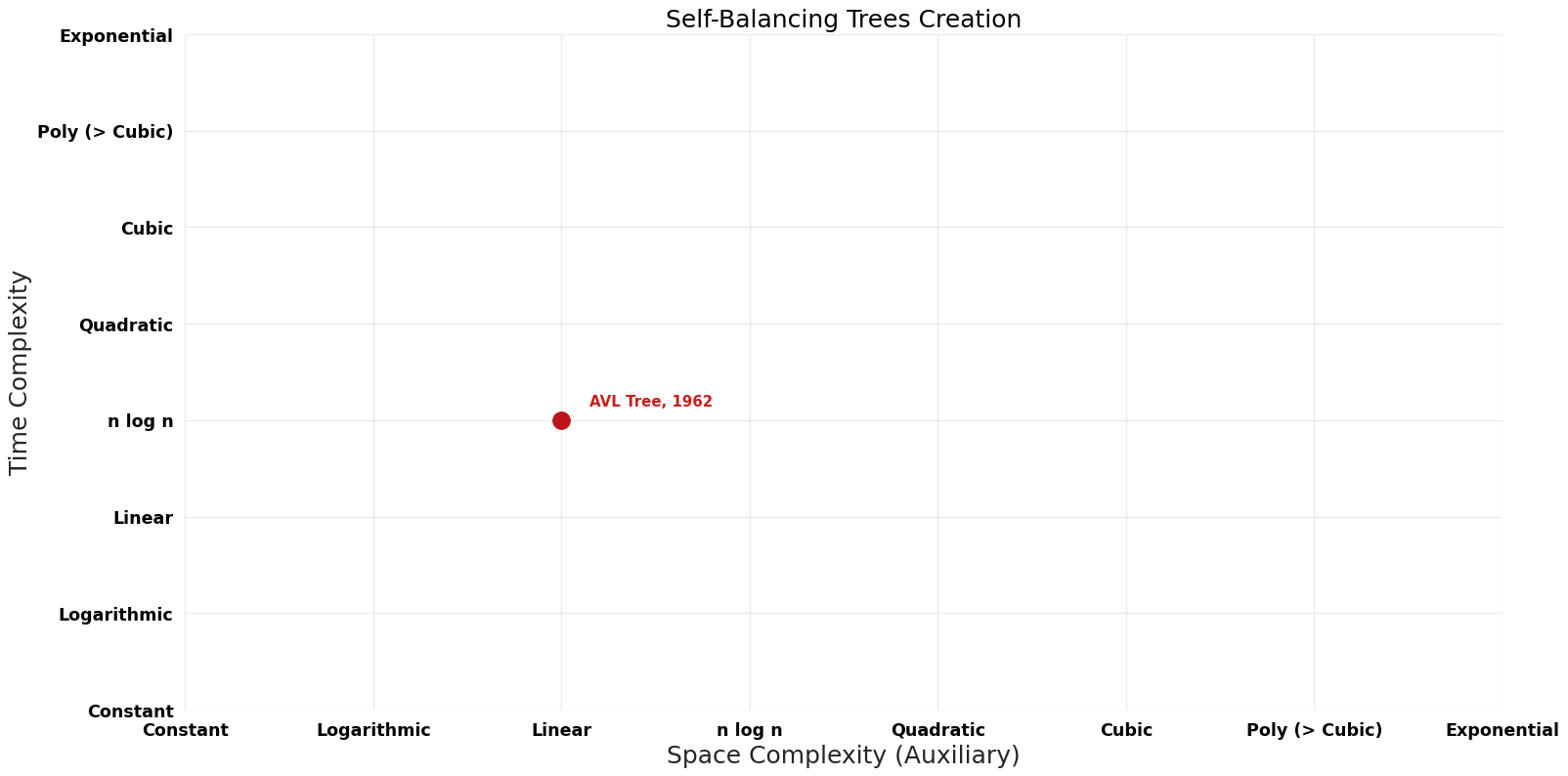
| [[AVL Tree ( Self-Balancing Trees Creation)|AVL Tree]] || 1962 || $O( | | [[AVL Tree ( Self-Balancing Trees Creation)|AVL Tree]] || 1962 || $O(n \log n)$ || $O(n)$ || Exact || Deterministic || | ||
|- | |- | ||
| [[Guibas, Sedgewick Red-Black Tree ( Self-Balancing Trees Creation)|Guibas, Sedgewick Red-Black Tree]] || 1972 || $O( | | [[Guibas, Sedgewick Red-Black Tree ( Self-Balancing Trees Creation)|Guibas, Sedgewick Red-Black Tree]] || 1972 || $O(n \log n)$ || $O(n)$ || Exact || Deterministic || [https://ieeexplore.ieee.org/document/4567957 Time] | ||
|- | |- | ||
| [[Hopcroft 2-3 Tree ( Self-Balancing Trees Creation)|Hopcroft 2-3 Tree]] || 1970 || $O( | | [[Hopcroft 2-3 Tree ( Self-Balancing Trees Creation)|Hopcroft 2-3 Tree]] || 1970 || $O(n \log n)$ || $O(n)$ || Exact || Deterministic || | ||
|- | |- | ||
| [[Tarjan Splay Tree ( Self-Balancing Trees Creation)|Tarjan Splay Tree]] || 1985 || $O( | | [[Tarjan Splay Tree ( Self-Balancing Trees Creation)|Tarjan Splay Tree]] || 1985 || $O(n \log n)$ || $O(n)$ || Exact || Deterministic || | ||
|- | |- | ||
| [[Bayer, McCreight B-Tree ( Self-Balancing Trees Creation)|Bayer, McCreight B-Tree]] || 1970 || $O(n*b*log(n)$/log(b))? || $O(n)$ || Exact || Deterministic || | | [[Bayer, McCreight B-Tree ( Self-Balancing Trees Creation)|Bayer, McCreight B-Tree]] || 1970 || $O(n*b*\log(n)$/\log(b))? || $O(n)$ || Exact || Deterministic || | ||
|- | |- | ||
| [[Scapegoat Tree ( Self-Balancing Trees Creation)|Scapegoat Tree]] || 1989 || $O(nlogn)$ || $O(n)$ || Exact || Deterministic || [https://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.138.4859 Time] | | [[Scapegoat Tree ( Self-Balancing Trees Creation)|Scapegoat Tree]] || 1989 || $O(nlogn)$ || $O(n)$ || Exact || Deterministic || [https://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.138.4859 Time] | ||
Revision as of 08:24, 10 April 2023
Description
Create a self-balancing tree given a list of elements.
Parameters
$n$: size of tree
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| AVL Tree | 1962 | $O(n \log n)$ | $O(n)$ | Exact | Deterministic | |
| Guibas, Sedgewick Red-Black Tree | 1972 | $O(n \log n)$ | $O(n)$ | Exact | Deterministic | Time |
| Hopcroft 2-3 Tree | 1970 | $O(n \log n)$ | $O(n)$ | Exact | Deterministic | |
| Tarjan Splay Tree | 1985 | $O(n \log n)$ | $O(n)$ | Exact | Deterministic | |
| Bayer, McCreight B-Tree | 1970 | $O(n*b*\log(n)$/\log(b))? | $O(n)$ | Exact | Deterministic | |
| Scapegoat Tree | 1989 | $O(nlogn)$ | $O(n)$ | Exact | Deterministic | Time |
| Treap | 1989 | $O(nlogn)$ | $O(n)$ | Exact | Randomized | Time |
| Tango Tree | 2004 | $O(nlogn)$ | $O(n)$ | Exact | Deterministic | Time |
Time Complexity Graph
Space Complexity Graph
Time-Space Tradeoff
