1D Maximum Subarray (Maximum Subarray Problem)

Description

Given an array $A$ of length $n$, find $i, j$ with $1\leq i \leq j \leq n$ maximizing $\sum^j_{x=i} A(x)$, that is, find a contiguous subarray of $A$ of maximum sum

Related Problems

Generalizations: Maximum Subarray

Related: 2D Maximum Subarray, Maximum Square Subarray

Parameters

n: length of array

Table of Algorithms

Name	Year	Time	Space	Approximation Factor	Model	Reference
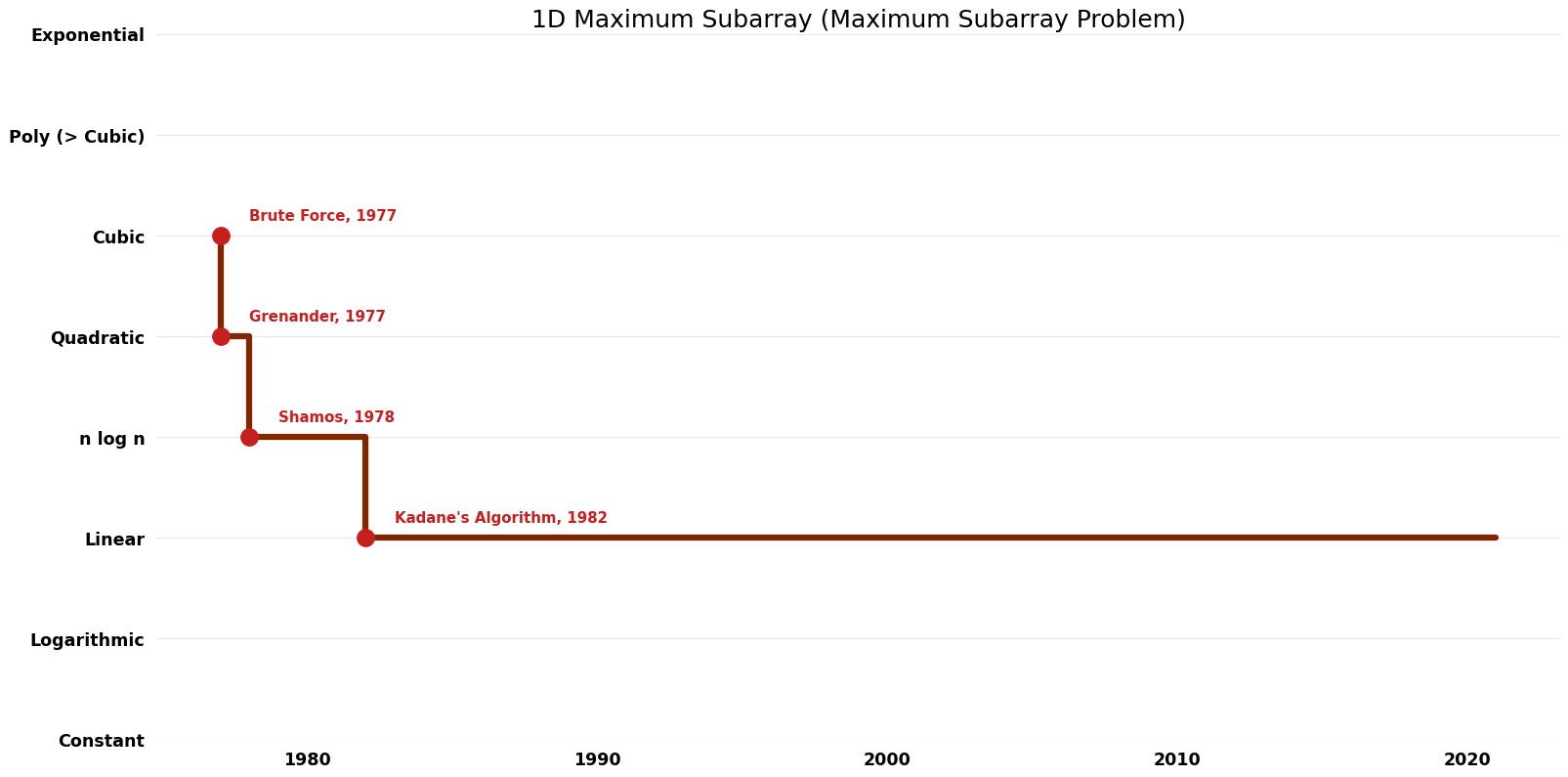
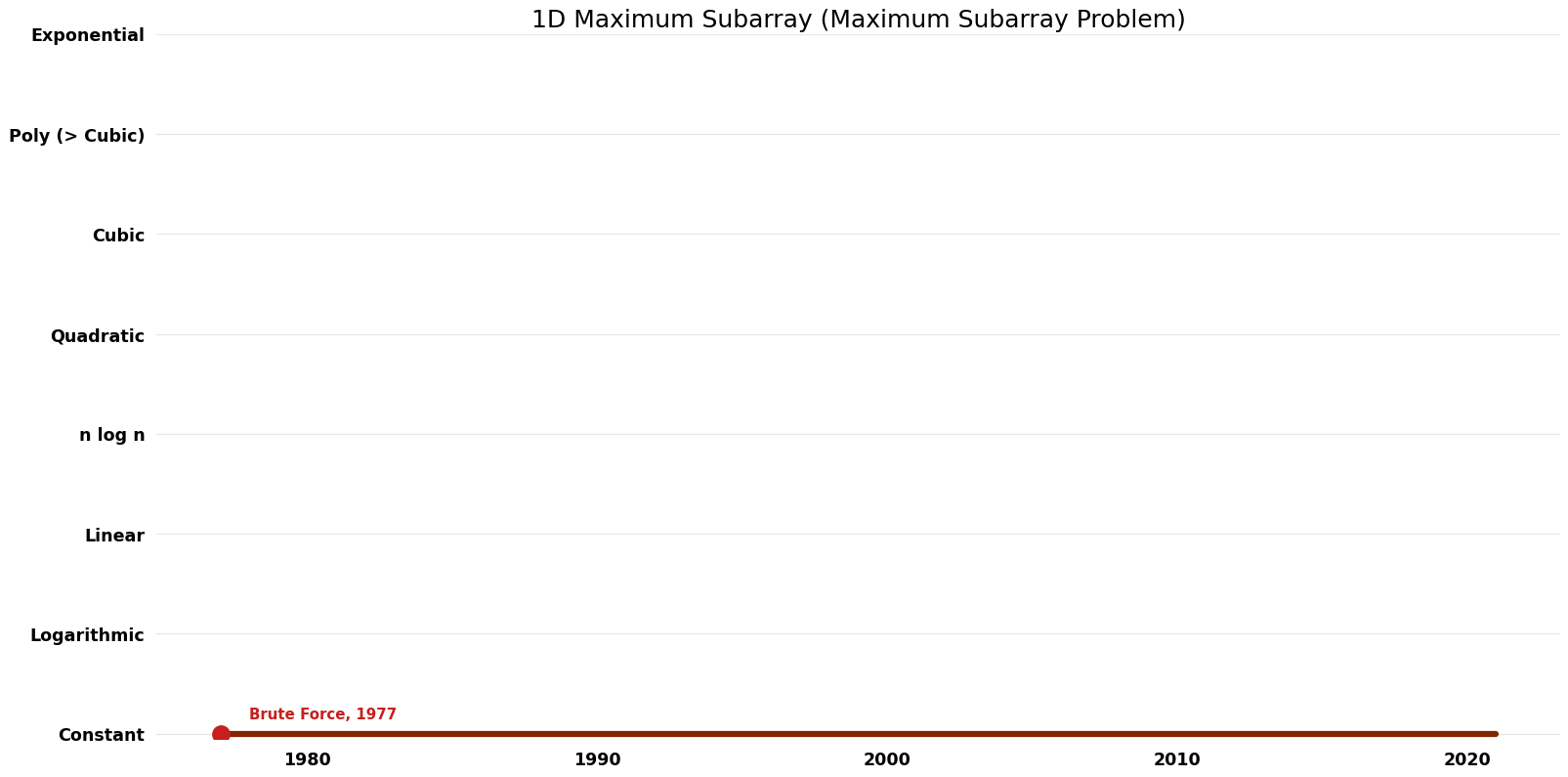
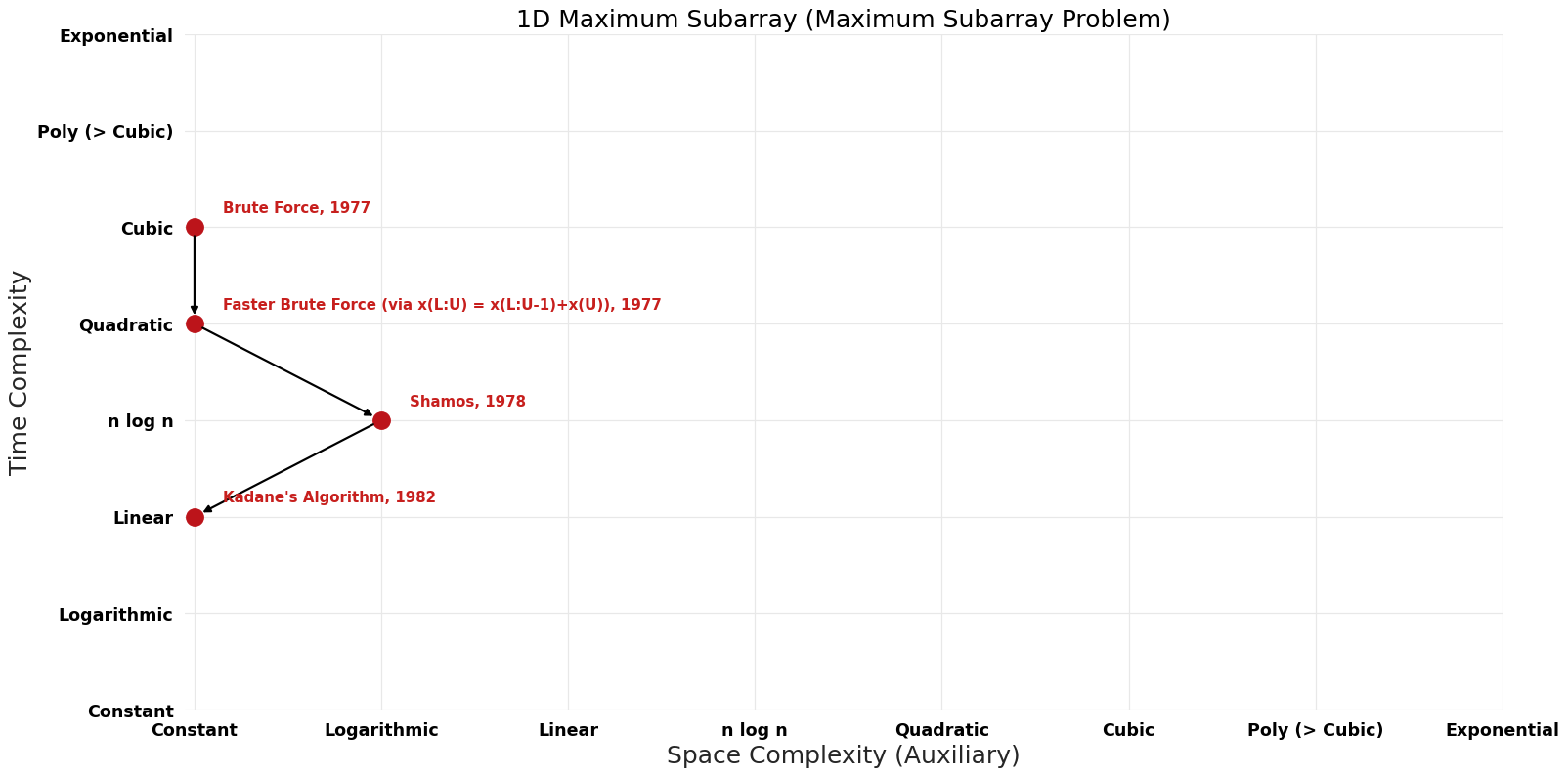
Brute Force	1977	$O(n^{3})$	$O({1})$ auxiliary	Exact	Deterministic
Grenander	1977	$O(n^{2})$	$O(n)$	Exact	Deterministic
Faster Brute Force (via x(L:U) = x(L:U-1)+x(U))	1977	$O(n^{2})$	$O({1})$ auxiliary	Exact	Deterministic	Time
Shamos	1978	$O(nlogn)$	$O(log n)$ auxiliary	Exact	Deterministic
Kadane's Algorithm	1982	$O(n)$	$O({1})$ auxiliary	Exact	Deterministic
Perumalla and Deo	1995	$O(log n)$	$O(n)$ auxiliary	Exact	Parallel	Time
Gries	1982	$O(n)$	$O({1})$ auxiliary	Exact	Deterministic	Time
Bird	1989	$O(n)$	$O({1})$ auxiliary	Exact	Deterministic	Time
Ferreira, Camargo, Song	2014	$O(log n)$	$O(n)$ auxiliary	Exact	Parallel	Time

Time Complexity Graph

Space Complexity Graph

Pareto Frontier Improvements Graph