Maximum Likelihood Methods in Unknown Latent Variables (Maximum Likelihood Methods in Unknown Latent Variables)
Jump to navigation
Jump to search
Description
In this problem, the goal is to compute maximum-likelihood estimates when the observations can be viewed as incomplete data.
Parameters
$n$: number of observations in sample
$r$: number of parameters + latent variables
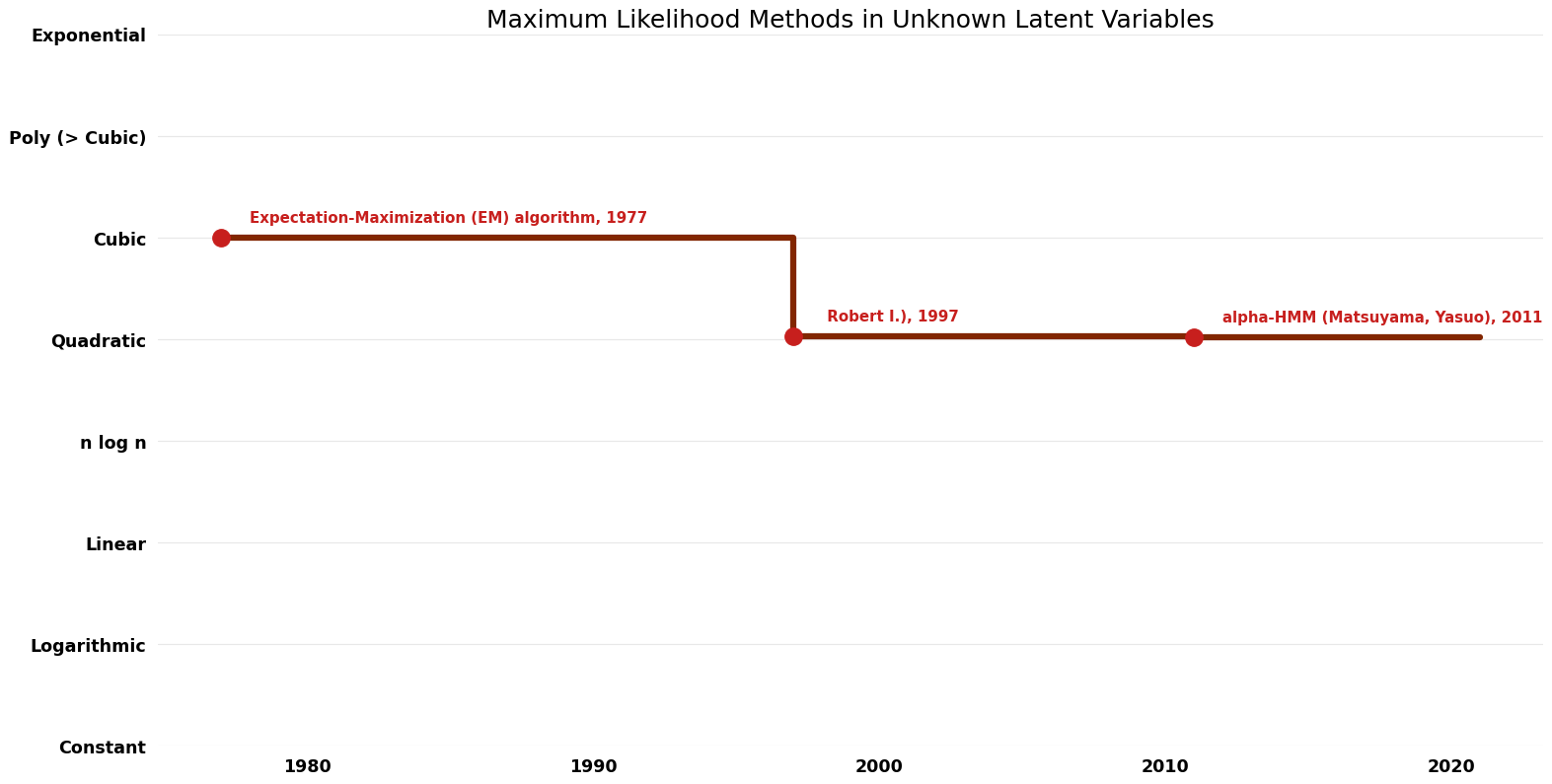
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Expectation-Maximization (EM) algorithm | 1977 | $O(n^{3})$ | $O(n+r)$? | Exact | Deterministic | Time |
| EM with Quasi-Newton Methods (Jamshidian; Mortaza; Jennrich; Robert I.) | 1997 | $O(n^{2} \log^{3} n)$ | $O(n+r^{2})$? | Exact | Deterministic | Time |
| Parameter-expanded expectation maximization (PX-EM) | 1998 | $O(n^{3})$ | $O(n+r)$? | Exact | Deterministic | Time |
| Expectation conditional maximization (ECM) | 1993 | $O(n^{3})$ | $O(n+r)$? | Exact | Deterministic | Time |
| Expectation conditional maximization either (ECME) (Liu; Chuanhai; Rubin; Donald B) | 1994 | $O(n^{3})$ | $O(n+r)$? | Exact | Deterministic | Time |
| α-EM Algorithm | 2003 | $O(n^{3})$ | $O(n+r)$? | Exact | Deterministic | Time |
| Shaban; Amirreza; Mehrdad; Farajtabar | 2015 | $O(n^{2} \log^{2} n)$ | $O(kd+d^{3})$?? | Exact | Deterministic | Time |
| alpha-HMM (Matsuyama, Yasuo) | 2011 | $O(n^{2} \log^{2} n)$ | Exact | Deterministic | Time |