Integer Maximum Flow (Maximum Flow)
Jump to navigation
Jump to search
Description
Maximum flow problems involve finding a feasible flow through a flow network that is maximum. In this variant, the capacities must be integers.
Related Problems
Generalizations: Non-Integer Maximum Flow
Subproblem: Unweighted Maximum Flow
Related: st-Maximum Flow, Non-integer Maximum Flow, Minimum-Cost Flow, All-Pairs Maximum Flow, Maximum Local Edge Connectivity
Parameters
V: number of vertices
E: number of edges
U: maximum edge capacity
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Ford & Fulkerson | 1955 | Exact | Deterministic | Time & Space | ||
| Dinitz | 1970 | Exact | Deterministic | Time & Space | ||
| Edmonds & Karp | 1972 | Exact | Deterministic | Time & Space | ||
| Karzanov | 1974 | Exact | Deterministic | Time & Space | ||
| Galil & Naamad | 1980 | Exact | Deterministic | Time & Space | ||
| Dantzig | 1951 | Exact | Deterministic | |||
| Dinitz (with dynamic trees) | 1973 | Exact | Deterministic | Time | ||
| Cherkassky | 1977 | Exact | Deterministic | Time & Space | ||
| Sleator & Tarjan | 1983 | Exact | Deterministic | Time | ||
| Goldberg & Tarjan | 1986 | Exact | Deterministic | Time | ||
| Ahuja & Orlin | 1987 | Exact | Deterministic | Time | ||
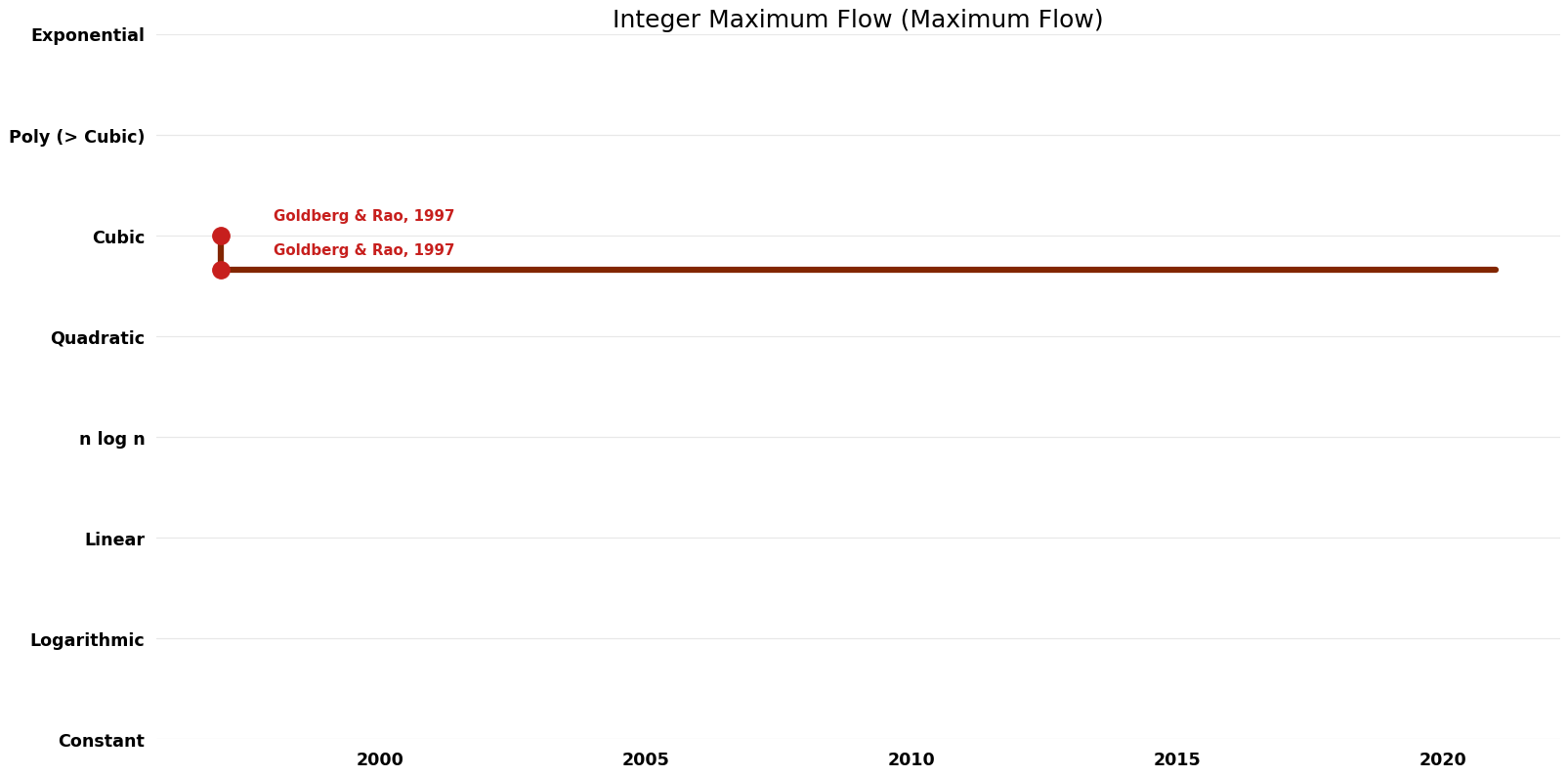
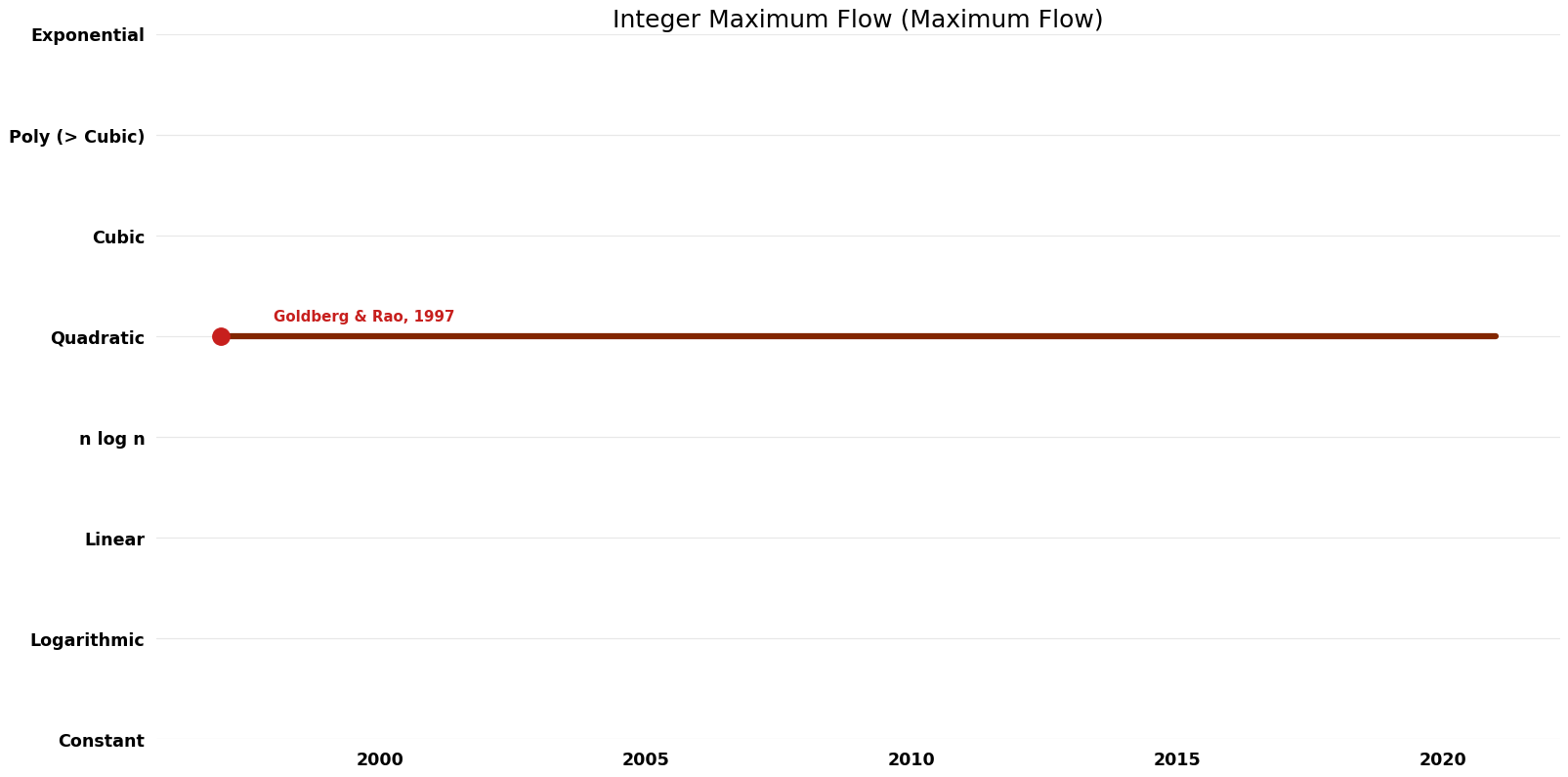
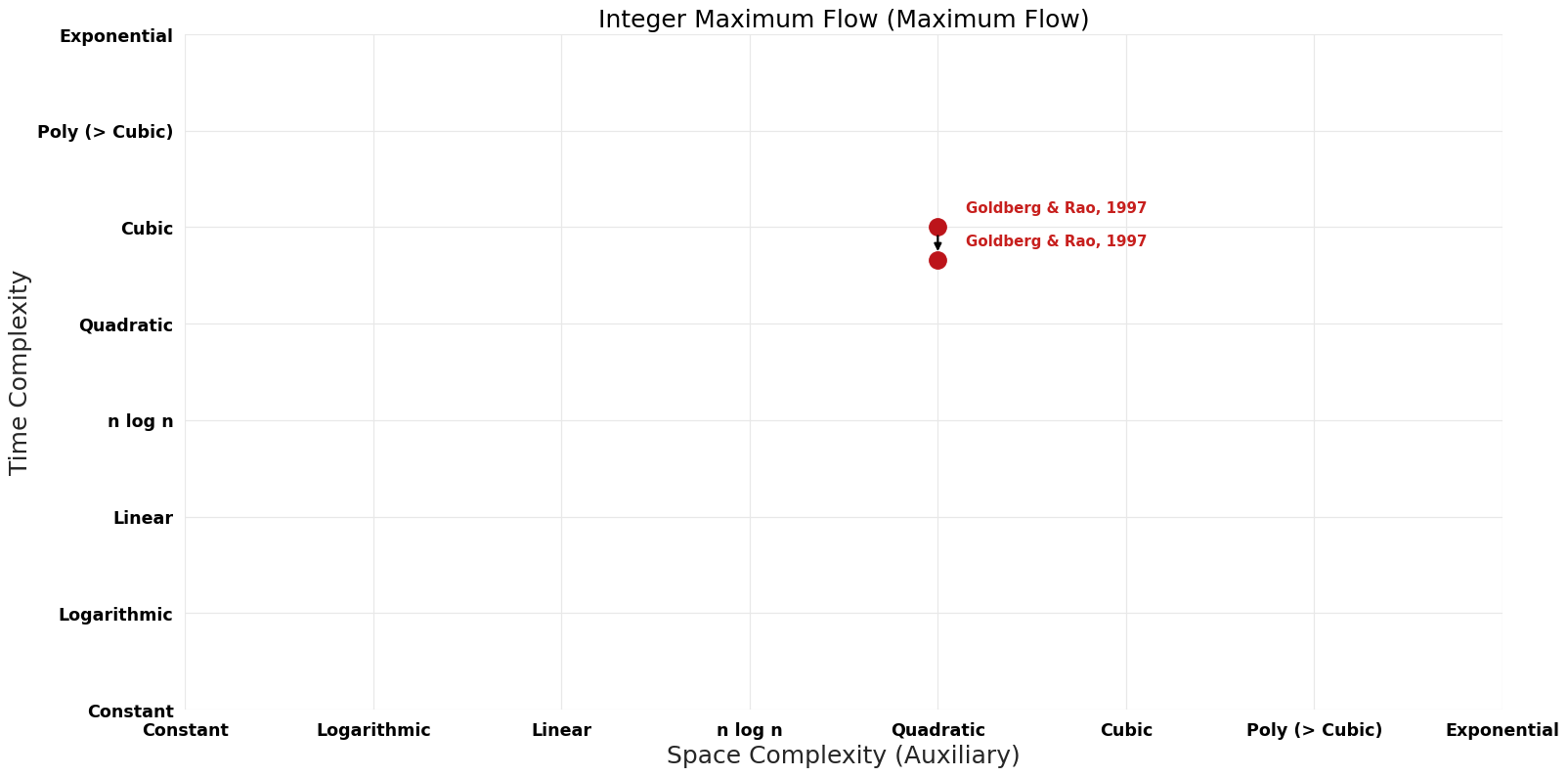
| Goldberg & Rao | 1997 | Exact | Deterministic | Time | ||
| Goldberg & Rao | 1997 | Exact | Deterministic | Time | ||
| Ahuja et al. | 1987 | Exact | Deterministic | Time | ||
| MKM Algorithm | 1978 | Exact | Deterministic | Time & Space | ||
| Galil | 1978 | Exact | Deterministic | Time & Space | ||
| Shiloach | 1981 | Exact | Parallel | Time | ||
| Gabow | 1985 | Exact | Deterministic | Time | ||
| Lee, Sidford | 2014 | Exact | Deterministic | Time | ||
| Madry | 2016 | Exact | Deterministic | Time | ||
| Kathuria, Liu, Sidford | 2020 | 1+eps | Deterministic | Time | ||
| Kathuria, Liu, Sidford | 2020 | Exact | Deterministic | Time | ||
| Brand et al | 2021 | Exact | Randomized | Time | ||
| Gao, Liu, Peng | 2021 | Exact | Deterministic | Time | ||
| Chen et al | 2022 | Exact | Deterministic | Time | ||
| Goldberg & Rao (Parallel) | 1997 | Exact | Parallel | Time & Space | ||
| Goldberg & Rao (Parallel) | 1997 | Exact | Parallel | Time & Space |