3-Graph Coloring (Graph Coloring)
Jump to navigation
Jump to search
Description
In this case, we wish to determine whether or not a graph is 3-colorable.
Related Problems
Generalizations: k-Graph Coloring
Related: Chromatic Number, 2-Graph Coloring, 4-Graph Coloring, 5-Graph Coloring, #k-Graph Coloring, #2-Graph Coloring, #3-Graph Coloring, #4-Graph Coloring, #5-Graph Coloring
Parameters
$n$: number of vertices
$m$: number of edges
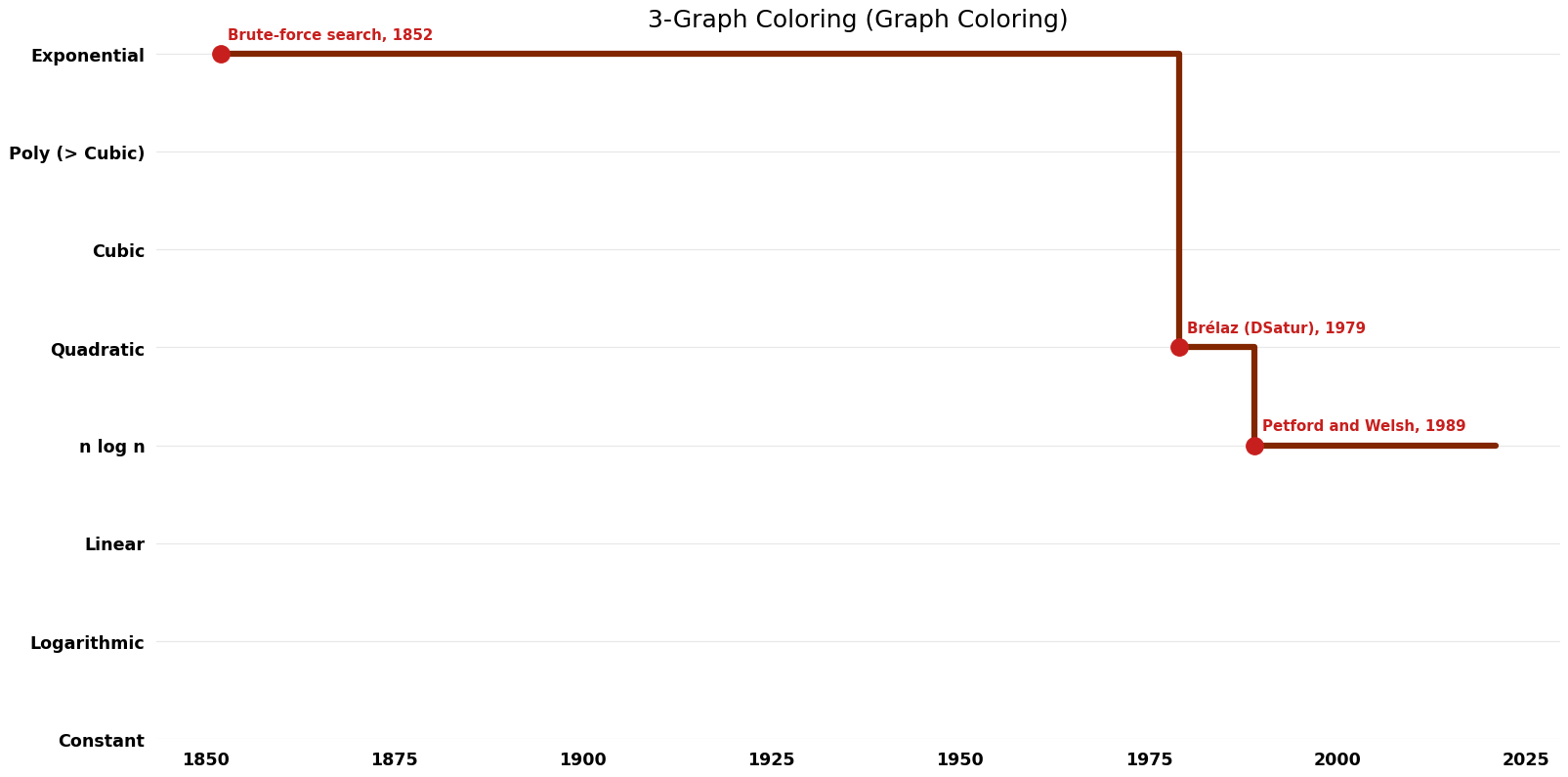
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Brute-force search | 1852 | $O((m+n)*{3}^n)$ | $O(n)$ auxiliary | Exact | Deterministic | |
| Brélaz (DSatur) | 1979 | $O(n^{2})$ | $O(m+n)$ | Exact | Deterministic | Time |
| Petford and Welsh | 1989 | $O(n \log n)$ | $O(n)$ | Exact | Randomized | Time |
| Lawler | 1976 | $O(m*n*{3}^{(n/{3})}) ~ O(mn({1.445})^n)$ | $O(n)$ | Exact | Deterministic | Time |
| Schiermeyer | 1994 | $O({1.415}^n)$ | $O(nm+n^{2})$ loose bound, possibly $O(n+m)$? | Exact | Deterministic | Time |
| Beigel & Eppstein | 1995 | $O({1.3446}^n)$ | $O(n^{2})$? | Exact | Deterministic | Time |
| Beigel & Eppstein | 2000 | $O({1.3289}^n)$ | $O(n^{2})$? | Exact | Deterministic | Time |
| Robson | 1986 | $O({1.2108}^n)$ | Exact | Deterministic | Time | |
| Schöning | 1999 | $O({1.333}^n)$ | Exact | Randomized | Time | |
| Hirsch | 1998 | $O({1.239}^n)$ | Exact | Deterministic | Time | |
| Johnson | 1988 | $O({1.4422}^n)$ | Exact | Deterministic | Time | |
| Alon and Kahale | 1997 | $O({1.24}^n)$ | Exact | Deterministic | Time |
Time Complexity Graph
References/Citation
https://www.sciencedirect.com/science/article/pii/S0196677404001117?via%3Dihub