Bipartite Graph MCM (Maximum Cardinality Matching)
Jump to navigation
Jump to search
Description
The goal of maximum cardinality matching is to find a matching with as many edges as possible (equivalently: a matching that covers as many vertices as possible). Here, the graph is bipartite.
Related Problems
Generalizations: General Graph MCM
Subproblem: Planar Bipartite Graph Perfect Matching
Parameters
$V$: number of vertices
$E$: number of edges
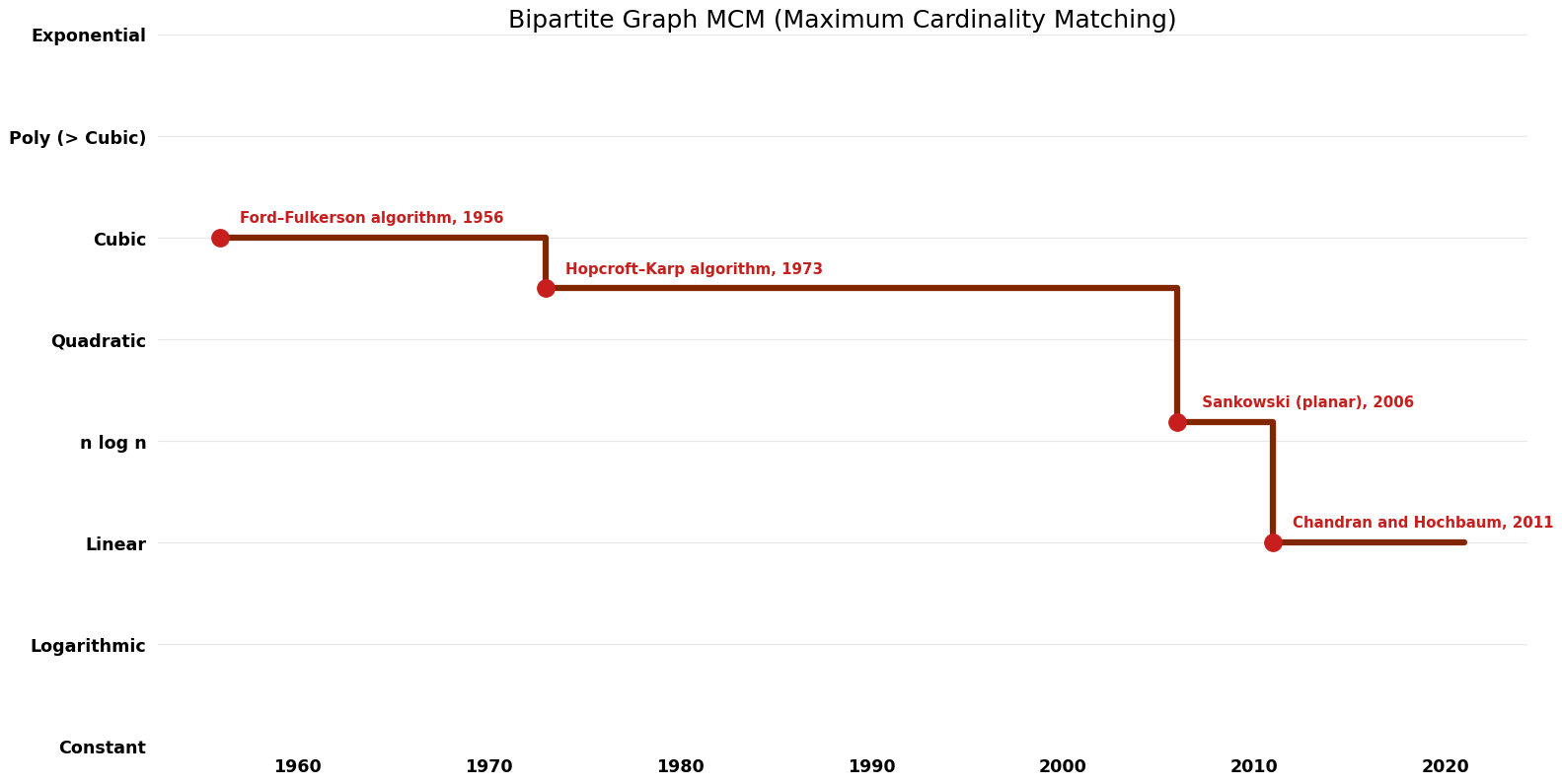
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Micali and Vazirani | 1980 | $O(V^{0.5} E)$ | $O(V)$ | Deterministic | Time & Space | |
| Ford–Fulkerson algorithm | 1956 | $O(VE)$ | $O(E)$ | Exact | Deterministic | Time |
| Hopcroft–Karp algorithm | 1973 | $O((V^{0.5})$E) | $O(V)$ | Exact | Deterministic | Time |
| Mucha; Sankowski (planar) | 2006 | $O(V^{(\omega/{2})$}) where omega is the exponent on matrix multiplication | $O(V \log V)$??? | Exact | Randomized | Time |
| Madry's algorithm | 2013 | $O(E^{10/7}*polylog(V)$) | $O(E + V)$ | Exact | Deterministic | Time |
| Chandran and Hochbaum | 2011 | $O(min(V*k, E)$+sqrt(k)*min(k^{2}, E)) | $O(E)$?? | Exact | Randomized | Time |
Time Complexity Graph
Reductions FROM Problem
| Problem | Implication | Year | Citation | Reduction |
|---|---|---|---|---|
| OuMv | assume: OMv then: there is no algorithm for solving incremental (or decremental) maximum cardinality bipartite matching with amortized time $O(n^{1-\epsilon})$ per insertion (or deletion) and $O(n^{2-\epsilon})$ time per query for any $\epsilon > {0}$ |
2016 | https://arxiv.org/abs/1602.06705 | link |