Constructing Suffix Trees (Constructing Suffix Trees)
Jump to navigation
Jump to search
Description
Let $T = t_1 t_2 \cdots t_n, be a string over an alphabet $\Sigma$. Each string $x$ such that $T = uxv$ for some (possibly empty) strings $u$ and $v$ is a substring of $T$, and each string $T_i = t_i \cdots t_n$, where $1 \leq i \leq n + 1$ is a suffix of $T$; in particular, $T_{n+1} = \epsilon$ is the empty suffix. The set of all suffixes of $T$ is denoted $\sigma(T)$. The suffix trie $STrie(T)$ of $T$ is a trie representing $\sigma(T)$.
Suffix tree $STree(T)$ of $T$ is a data structure that represents $STrie(T)$ in space linear in the length $|T|$ of $T$. This is achieved by representing only a subset $Q' \cup \{ \perp \}$ of the states of $STrie(T)$.
Parameters
$n$: length of string
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
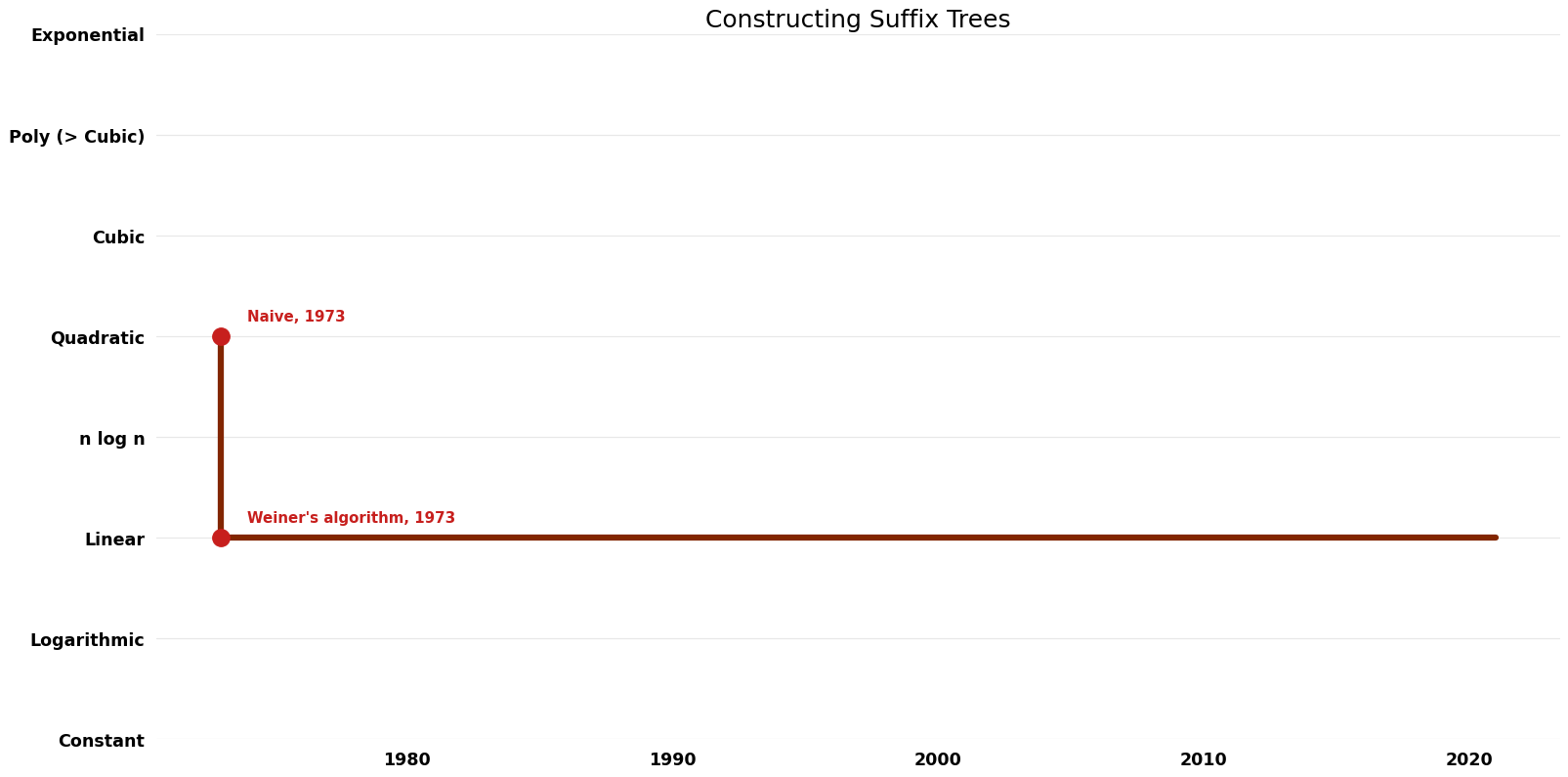
| Naive | 1973 | $O(n^{2})$ | $O(n)$ | Exact | Deterministic | |
| Weiner's algorithm | 1973 | $O(n)$ | $O(n)$ | Exact | Deterministic | Time |
| Pratt | 1973 | $O(n)$ | Exact | Deterministic | ||
| Ukkonen | 1995 | $O(n)$ | $O(n)$ | Exact | Deterministic | Time |
| Ukkonen and D. Wood | 1993 | $O(n^{2})$ | $O(n^{2})$ | Exact | Deterministic | Time & Space |
| Hariharan | 1997 | $O(log^{4}(n)$) | $O(n)$ | Exact | Parallel | Time & Space |
| Süleyman Cenk Sahinalp ; Uzi Vishkin | 1994 | $O(log^{2}(n)$) | $O(n^{({1}+\eps)})$ for any fixed eps>{0} | Exact | Parallel | Time & Space |
| Farach | 1997 | $O(\log n)$ | $O(n)$ | Exact | Randomized | Time & Space |
| Rytter | 2004 | $O(\log n)$ | $O(n)$ | Exact | Parallel | Time & Space |
| McCreight | 1976 | $O(n)$ | $O(n)$ | Exact | Deterministic | Time |