DAG Realization Problem (Graph Realization Problems)
Jump to navigation
Jump to search
Description
Given a sequence $S := (a_1, b_1), \ldots, (a_n, b_n)$ with $a_i, b_i \in \mathbb{Z}_0^+$, does there exist a directed acyclic graph (DAG) (no parallel arcs allowed) with labeled vertex set $V := \{v_1, \ldots , v_n\}$ such that for all $v_i \in V$ indegree and outdegree of $v_i$ match exactly the given numbers $a_i$ and $b_i$, respectively?
Related Problems
Generalizations: Digraph Realization Problem
Parameters
$n$: number of degree pairs
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
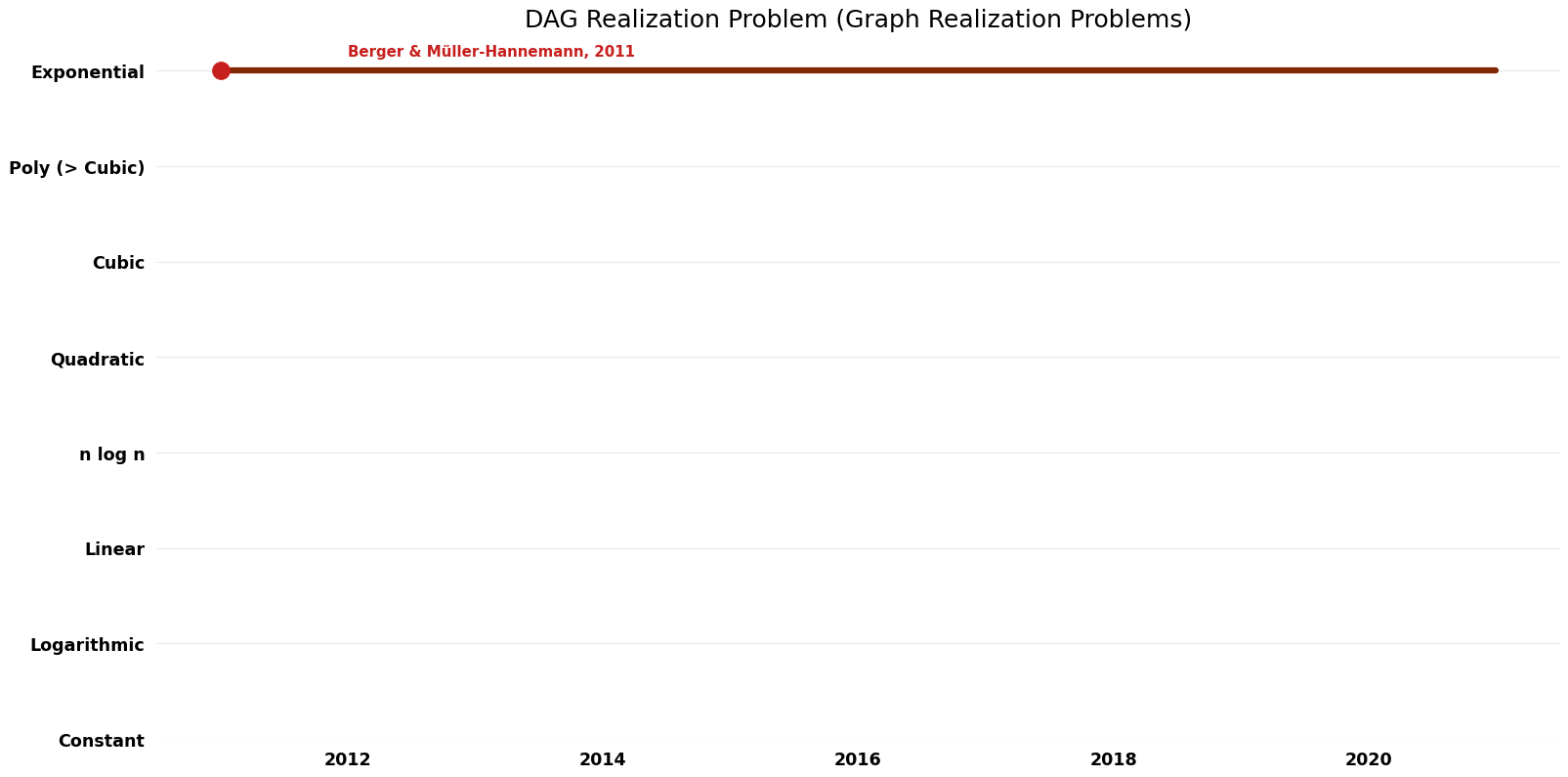
| Berger & Müller-Hannemann | 2011 | $O(\exp(n)$) | ? | Exact | Deterministic | Time |
Time Complexity Graph
References/Citation
https://link.springer.com/chapter/10.1007/978-3-642-30870-3_29