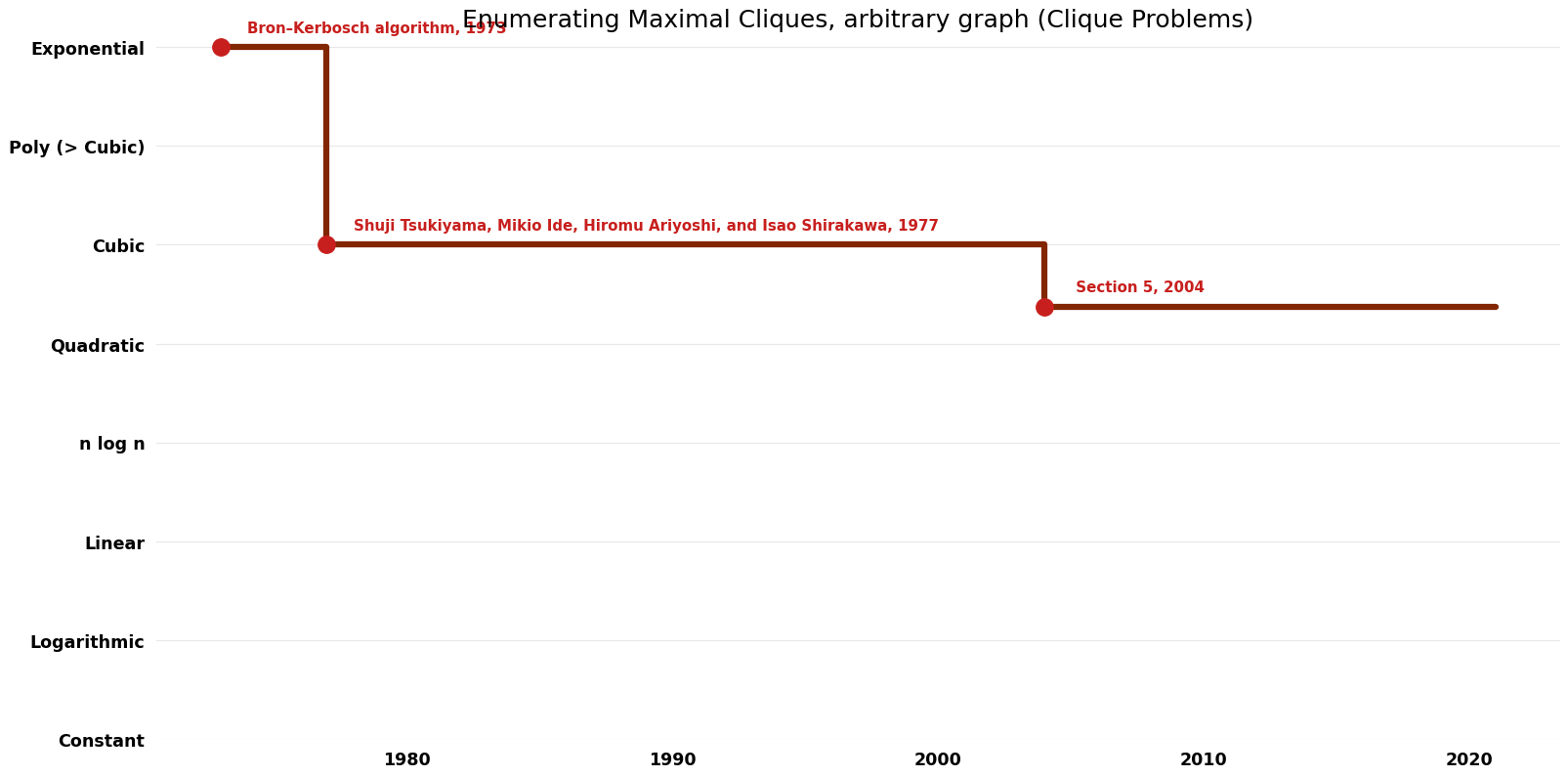
Enumerating Maximal Cliques, arbitrary graph (Clique Problems)
Jump to navigation
Jump to search
Description
A maximal clique (complete subgraph) is a clique that is not contained in any other clique. The goal here is to enumerate such maximal cliques in a given graph.
Related Problems
Related: k-Clique, Exact k-Clique, Min-Weight k-Clique, Max-Weight k-Clique
Parameters
$n$: number of vertices
$m$: number of edges
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Bron–Kerbosch algorithm | 1973 | $O({3}^{(n/{3})})$ | $O(n^{2})$? | Exact | Deterministic | Time |
| Akkoyunlu; E. A. | 1973 | $O({3}^{(n/{3})$}) | $O(n^{2})$? | Exact | Deterministic | Time |
| Tomita; Tanaka & Takahashi | 2006 | $O({3}^{(n/{3})$}) | $O(n^{2})$? | Exact | Deterministic | Time |
| Segundo; Artieda; Strash Parallel | 2011 | $O({3}^{(n/{3})})$ total work? (previously this cell said $O(n^{4})$) | $O(n^{2})$ auxiliary?? | Exact | Parallel | Time |
| David Eppstein, Maarten Löffler, Darren Strash | 2010 | $O(dn {3}^{(d/{3})})$ | $O(n^{2})$? | Exact | Deterministic | Time |
| Chiba and Nishizeki | 1985 | $O(a(G)*m)$ per clique | $O(m)$ | Exact | Deterministic | Time & Space |
| M. Chrobak and D. Eppstein | 1989 | $O(n d^{2} {2}^d)$ | $O(n)$? | Exact | Deterministic | Time |
| Shuji Tsukiyama, Mikio Ide, Hiromu Ariyoshi, and Isao Shirakawa | 1977 | $O(nm)$ per clique | $O(m)$ | Exact | Deterministic | Time |
| Kazuhisa Makino, Takeaki Uno; Section 5 | 2004 | $O(n^{\omega})$ per clique where omega is the exponent on matrix multiplication | $O(n^{2})$ | Exact | Deterministic | Time & Space |
| Kazuhisa Makino, Takeaki Uno; Section 6 | 2004 | $O(delta^{4})$ | $O(n+m)$ auxiliary(?) | Exact | Deterministic | Time & Space |