Longest Common Subsequence (Longest Common Subsequence)
Jump to navigation
Jump to search
Description
The longest common subsequence (LCS) problem is the problem of finding the longest subsequence common to all sequences in a set of sequences (often just two sequences).
Related Problems
Subproblem: Longest Common Substring with don't cares
Parameters
$n$: length of the longer input string
$m$: length of the shorter input string
$r$: length of the LCS
$s$: size of the alphabet
$p$: the number of dominant matches (AKA number of minimal candidates), i.e. the total number of ordered pairs of positions at which the two sequences match
Table of Algorithms
Currently no algorithms in our database for the given problem.
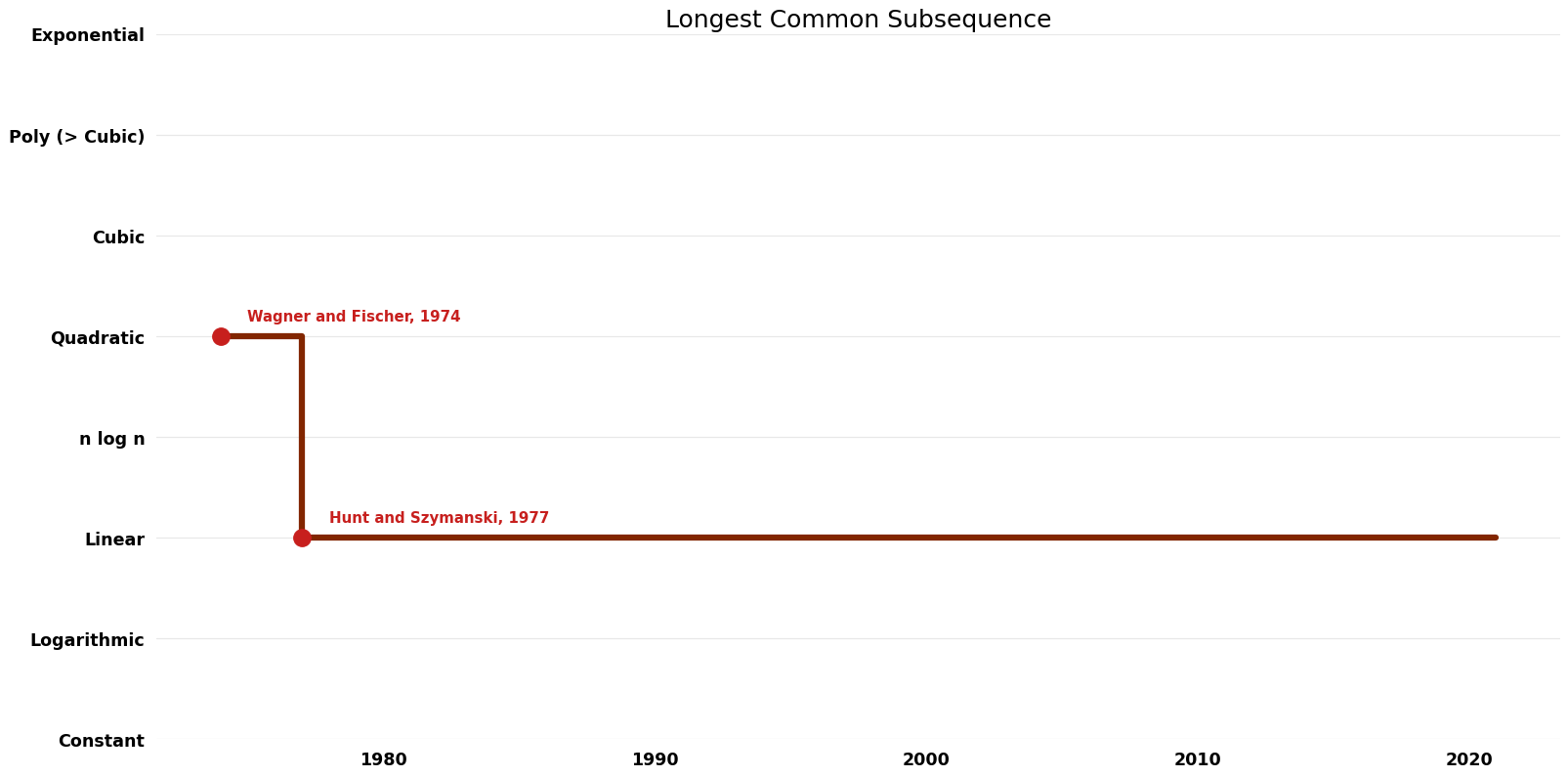
Time Complexity Graph
Reductions FROM Problem
| Problem | Implication | Year | Citation | Reduction |
|---|---|---|---|---|
| UOV | If: to-time: $O((nm)^{({1}-\epsilon)})$, where $|x| = O(nd)$ and $|y| = O(md)$ Then: from-time: $O((nm)^{({1}-\epsilon/{2})})$ |
2015 | https://arxiv.org/pdf/1502.01063.pdf | link |
References/Citation
https://link.springer.com/chapter/10.1007/978-3-662-43948-7_4