Multiplication (Multiplication)
Jump to navigation
Jump to search
Description
Multiplication is one of the four elementary mathematical operations of arithmetic; with the others being addition; subtraction and division. Given two $n$-bit integers, compute their product, which should be a $2n$-bit integer.
Parameters
$n$: length of one of the integers, in bits
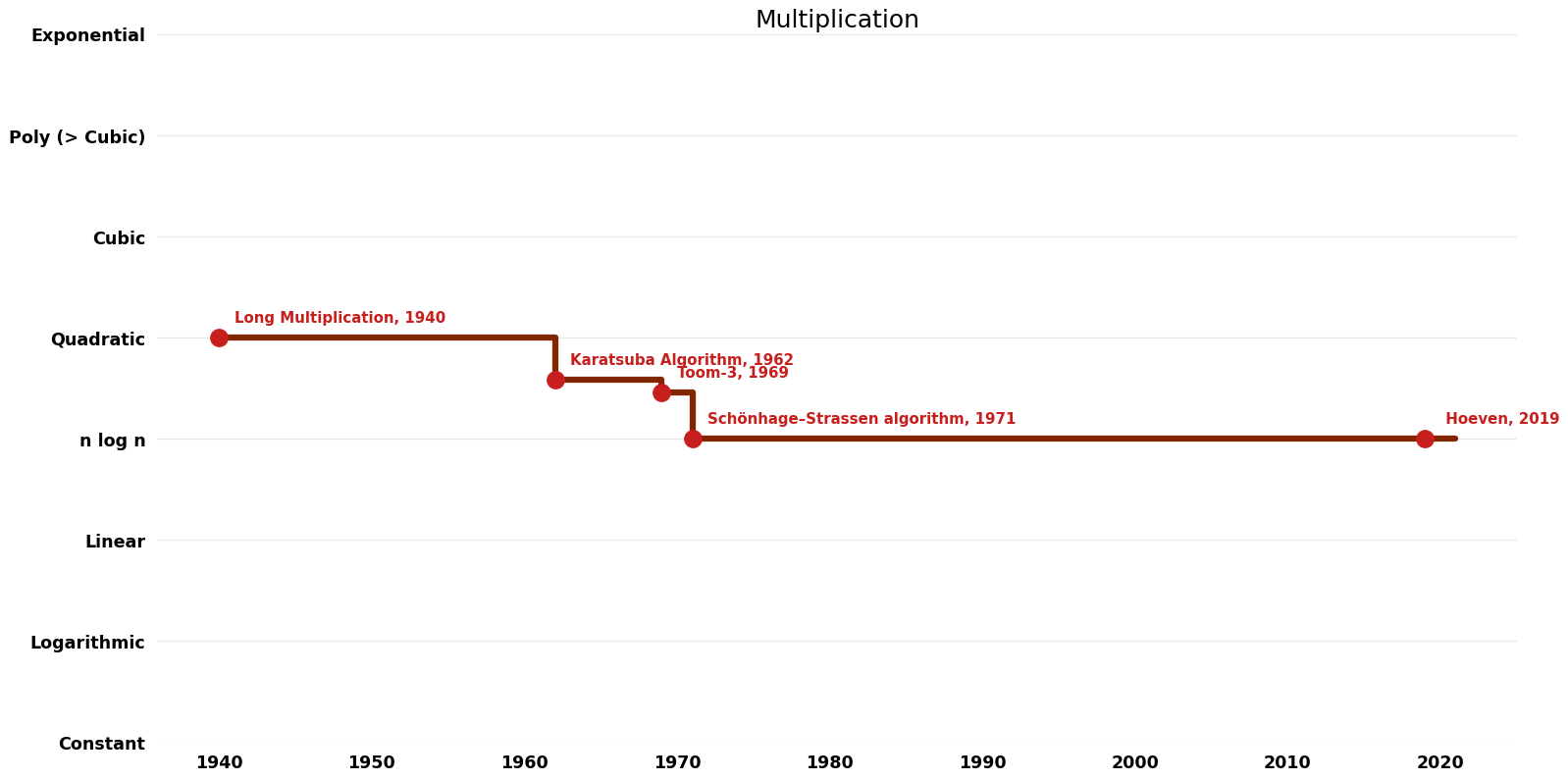
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Karatsuba Algorithm | 1962 | $O(n^{1.{5}8})$ | $O(n)$ | Exact | Deterministic | Time |
| Toom-3 | 1969 | $O(n^{1.{4}6})$ | $O(n)$ | Exact | Deterministic | Time |
| Long Multiplication | 1940 | $O(n^{2})$ | $O(n)$ | Exact | Deterministic | |
| Schönhage–Strassen algorithm | 1971 | $O(n \log n \log\log n)$ | $O(n)$ auxiliary? | Exact | Deterministic | Time |
| Furer's algorithm | 2007 | $O(n \log n {2}^{O(\log*n)})$ | $O(n)$ auxiliary? | Exact | Deterministic | Time |
| De | 2008 | $O(n \log n {2}^{O(\log*n)})$ | $O(n)$ auxiliary? | Exact | Deterministic | Time |
| Harvey; Hoeven | 2019 | $O(n \log n)$ | $O(n)$ auxiliary?? | Exact | Deterministic | Time |
| Harvey; Hoeven; Lecerf | 2015 | $O(n \log n {2}^{({3} \log*n)})$ | $O(n)$ auxiliary?? | Exact | Deterministic | Time |
| Covanov and Thomé | 2015 | $O(n \log n {2}^{O(\log*n)})$ | $O(n)$ auxiliary?? | Exact | Deterministic | Time |
| Covanov and Thomé | 2016 | $O(n \log n {2}^{({3} \log*n)})$ | $O(n)$ auxiliary?? | Exact | Deterministic | Time |
| Harvey; Hoeven; Lecerf | 2018 | $O(n \log n {2}^{({2} \log*n)})$ | $O(n)$ auxiliary?? | Exact | Deterministic | Time |