Non-Comparison Sorting

Description

A sorting algorithm is an algorithm that puts elements of a list in a certain order, not using comparisons between elements (so elements are typically integers or real numbers).

Related Problems

Generalizations: Sorting

Related: Comparison Sorting

Parameters

n: size of list

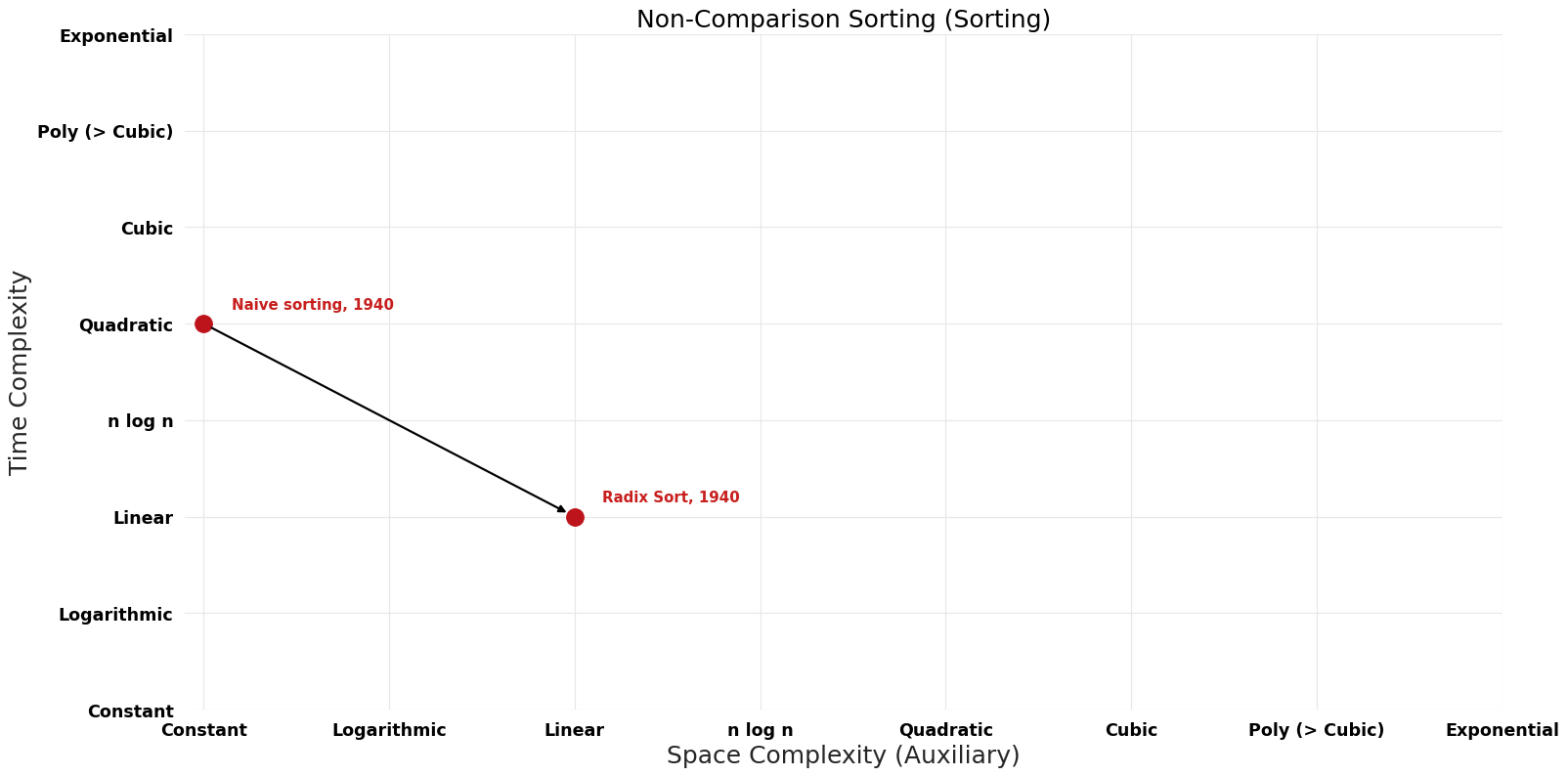
Table of Algorithms

Name	Year	Time	Space	Approximation Factor	Model	Reference
Counting Sort	1954	$O(n+k)$	$O(n+k)$	Exact	Deterministic	Time
Bucket Sort	1940	$O( n² )$	$O(n)$	Exact	Deterministic
Radix Sort	1940	$O(wn)$	$O(w+n)$	Exact	Deterministic
Naive sorting	1940	$O( n² )$	$O({1})$ (in-situ)	Exact	Deterministic
Flash Sort	1998	$O(n^{2})$	$O(n)$	Exact	Deterministic	Time
Bead Sort	2002	$O(n)$	$O(n^{2})$	Exact	Deterministic	Time
Burst Sort	2004	$O(wn)$	$O(wn)$	Exact	Deterministic	Time
Spreadsort	2002	$O(n*log n)$	$O(n)$?	Exact	Deterministic	Time
Spaghetti Sort Parallel Implementation	1984	$O(n)$	$O({1})$ auxiliary? per processor?	Exact	Parallel	Time

Time Complexity graph

Space Complexity graph

Pareto Decades graph