Comparison Sorting (Sorting)
Jump to navigation
Jump to search
Description
A sorting algorithm is an algorithm that puts elements of a list in a certain order, using comparisons between elements.
Related Problems
Generalizations: Sorting
Related: Non-Comparison Sorting
Parameters
$n$: size of list
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
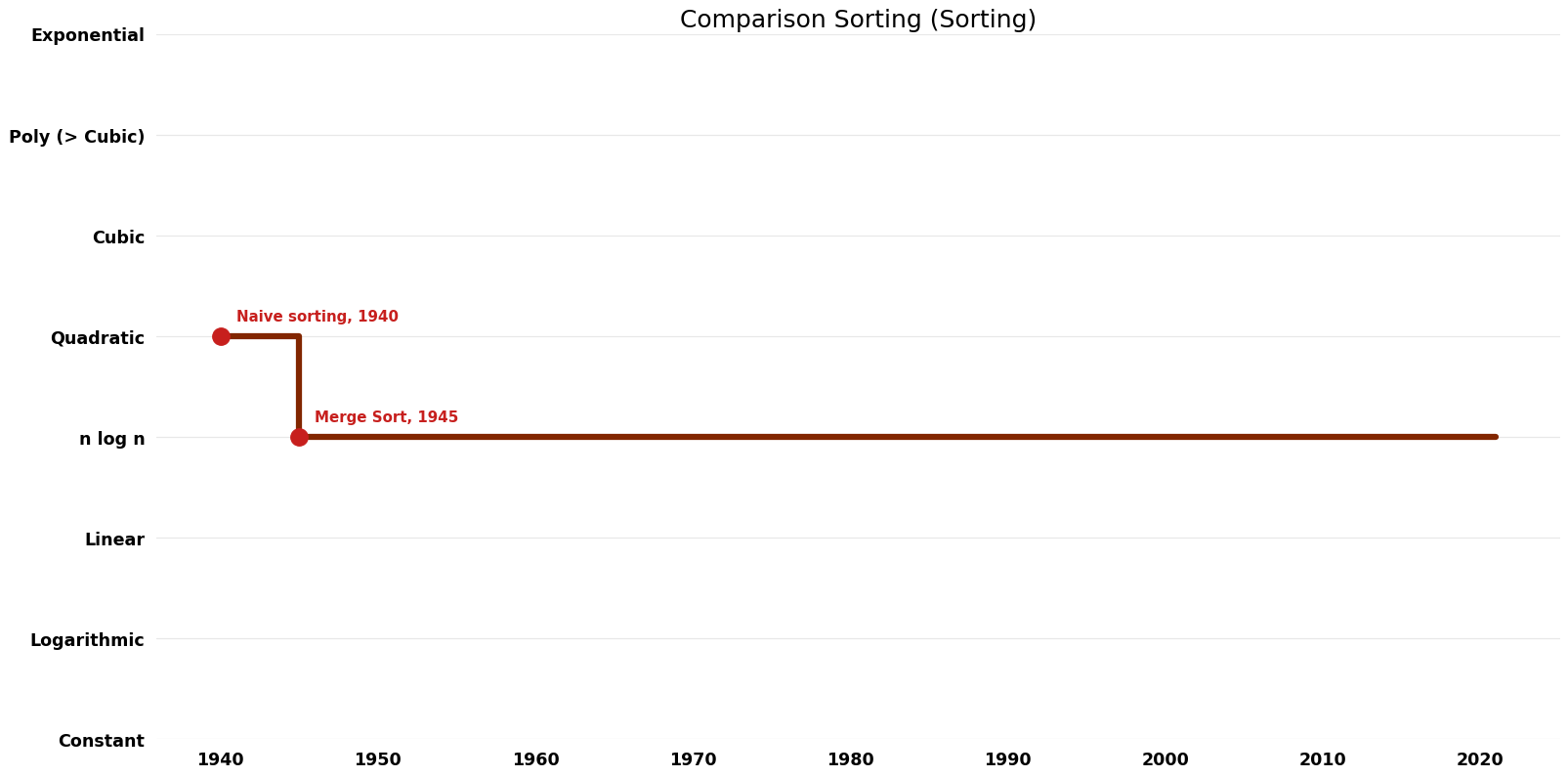
| Naive sorting | 1940 | $O(n^{2})$ | $O({1})$ (in-situ) | Exact | Deterministic | |
| Selection Sort | 1962 | $O(n^{2})$ | $O({1})$ (in-situ) | Exact | Deterministic | |
| Merge Sort | 1945 | $O(n \log n)$ | $O(n)$ | Exact | Deterministic | |
| Bubble Sort | 1956 | $O(n^{2})$ | $O({1})$ (in-situ) | Exact | Deterministic | |
| Intro Sort | 1997 | $O(n \log n)$ | $O(logn)$ | Exact | Deterministic | Time |
| Heap Sort | 1964 | $O(n \log n)$ | $O({1})$ (in-situ) | Exact | Deterministic | Time |
| Counting Sort | 1954 | $O(n+k)$ | $O(n+k)$ | Exact | Deterministic | Time |
| Bucket Sort | 1940 | $O( n² )$ | $O(n)$ | Exact | Deterministic | |
| Radix Sort | 1940 | $O(wn)$ | $O(w+n)$ | Exact | Deterministic | |
| Tree sort | 1986 | $O(n \log n)$ | $O(n)$ | Exact | Deterministic | Time |
| Quick Sort | 1961 | $O(n^{2})$ | $O(\log n)$ | Exact | Deterministic | Time & Space |
| Tim Sort | 2002 | $O(n logn)$ | $O(n)$ | Exact | Deterministic | |
| Cube Sort Parallel Implementation | 1992 | $O(n logn)$ | $O(n)$ | Exact | Parallel | Time |
| Shell Sort (Shell) | 1959 | $O(n^{2})$ | $O({1})$ | Exact | Deterministic | Time |
| Shell Sort (Frank & Lazarus) | 1960 | $O(n^{1.5})$ | $O({1})$ | Exact | Deterministic | Time |
| Shell Sort (Pratt) | 1971 | $O(n \log^{2} n)$ | $O({1})$ | Exact | Deterministic | Time |
| Shell Sort (Sedgewick) | 1986 | $O(n^{1.{3}3})$ | $O({1})$ | Exact | Deterministic | Time |
| Bitonic Merge Sort Parallel Implementation | 1968 | $O(\log^{2} n)$ | $O({1})$ | Exact | Parallel | Time |
| Thorup's Sorting Algorithm | 2002 | $O(n \log \log n)$ | $O(n)$ | Exact | Deterministic | Time & Space |
| Naive sorting | 1940 | $O(n^{2})$ | $O({1})$ | Exact | Deterministic | |
| Flash Sort | 1998 | $O(n^{2})$ | $O(n)$ | Exact | Deterministic | Time & Space |
| Bead Sort | 2002 | $O(n)$ | $O(n^{2})$ | Exact | Deterministic | Time |
| Burst Sort | 2004 | $O(wn)$ | $O(wn)$ | Exact | Deterministic | Time |
| Spreadsort | 2002 | $O(n \log n)$ | $O(n)$? | Exact | Deterministic | Time |
| Odd Even Sort Parallel Implementation | 1972 | $O(n^{2})$ | $O({1})$ | Exact | Parallel | Time |
| Spaghetti Sort Parallel Implementation | 1984 | $O(n)$ | $O({1})$ auxiliary? per processor? | Exact | Parallel | Time |