Maximum Cut: Difference between revisions
Jump to navigation
Jump to search
(Created page with "{{DISPLAYTITLE:Maximum Cut (Maximum Cut)}} == Description == Given a graph $G=(V, E)$ with edge weights $c_e > 0$ for all $e\in E$, find a cut $\delta(W)$ such that $c(\delta(W)):=\Sigma_{e\in \dela(W)} c_e$ is as large as possible. == Parameters == <pre>n: number of vertices m: number of edges</pre> == Table of Algorithms == {| class="wikitable sortable" style="text-align:center;" width="100%" ! Name !! Year !! Time !! Space !! Approximation Factor !! Model !!...") |
No edit summary |
||
| Line 6: | Line 6: | ||
== Parameters == | == Parameters == | ||
n: number of vertices | |||
m: number of edges | |||
m: number of edges | |||
== Table of Algorithms == | == Table of Algorithms == | ||
Revision as of 12:03, 15 February 2023
Description
Given a graph $G=(V, E)$ with edge weights $c_e > 0$ for all $e\in E$, find a cut $\delta(W)$ such that $c(\delta(W)):=\Sigma_{e\in \dela(W)} c_e$ is as large as possible.
Parameters
n: number of vertices
m: number of edges
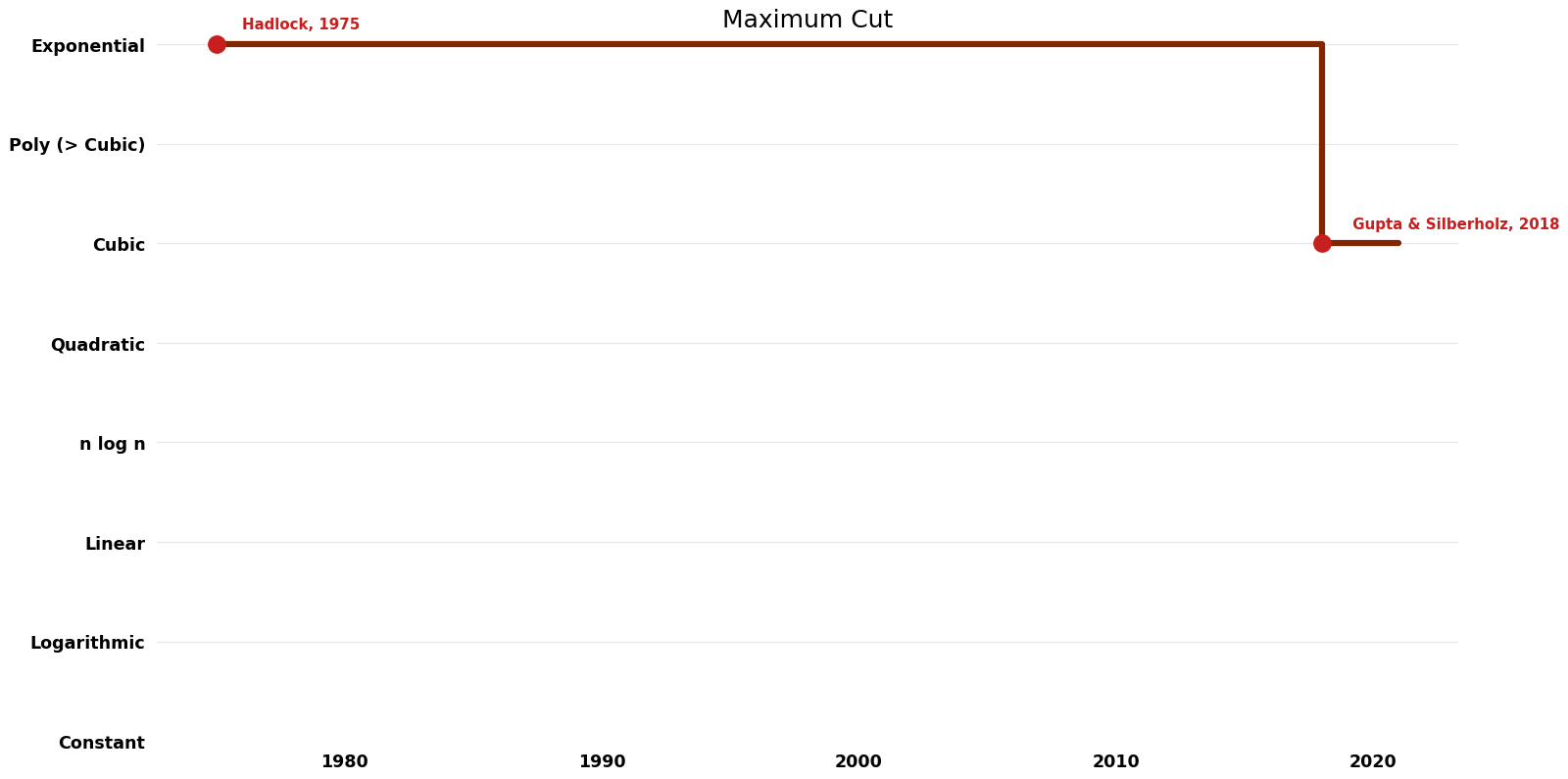
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Hadlock | 1975 | $O({2}^V)$ | Exact | Deterministic |
Time Complexity graph
