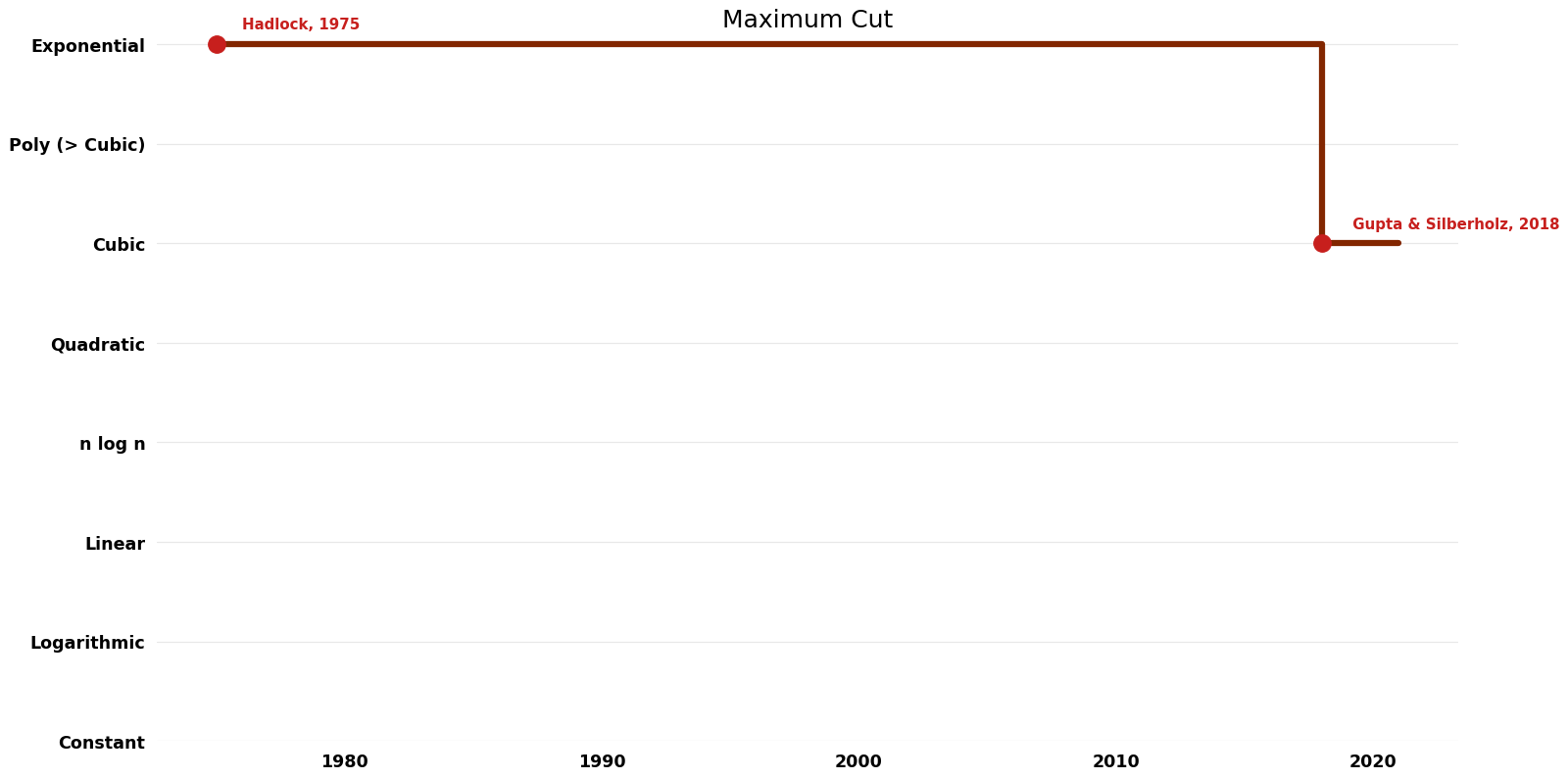
Maximum Cut (Maximum Cut)
Jump to navigation
Jump to search
Description
Given a graph $G=(V, E)$ with edge weights $c_e > 0$ for all $e\in E$, find a cut $\delta(W)$ such that $c(\delta(W)):=\Sigma_{e\in \dela(W)} c_e$ is as large as possible.
Parameters
$n$: number of vertices
$m$: number of edges
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Hadlock | 1975 | $O({2}^n)$ | Exact | Deterministic | ||
| Motwani & Raghavan | 1995 | $O(n)$? | $O(n)$ | 0.5 | Randomized | Time |
| Mitzenmacher & Upfal | 2005 | $O(mn)$? | $O(n)$ | 0.5 | Deterministic | Time |
| Khuller; Raghavachari & Young, "Greedy Methods" | 2007 | $O(n^{2})$? | $O(n)$ | 0.5 | Deterministic | Time |
| Ausiello et al. | 2003 | $O(n^{3} \log m)$ | $O(n^{2})$? | ~0.878; assuming this is the goemans-williamson algorithm | Deterministic | Time |
| Dunning; Gupta & Silberholz | 2018 | $O(mn)$ | Exact | Deterministic | Time |