Reporting all intersection points, generalized segments: Difference between revisions
Jump to navigation
Jump to search
(Created page with "{{DISPLAYTITLE:Reporting all intersection points, generalized segments (Line segment intersection)}} == Description == In this case, the segments are generalized (i.e. have algebraic degree ≥1); we still wish to report all points of intersection. == Related Problems == Subproblem: Reporting all intersection points, line segments Related: Reporting all intersection points, convex polygons, Reporting all intersection points, general polygons, Counting...") |
No edit summary |
||
| Line 12: | Line 12: | ||
== Parameters == | == Parameters == | ||
n: number of line segments | |||
k: number of points of intersection | |||
k: number of points of intersection | |||
== Table of Algorithms == | == Table of Algorithms == | ||
Revision as of 12:02, 15 February 2023
Description
In this case, the segments are generalized (i.e. have algebraic degree ≥1); we still wish to report all points of intersection.
Related Problems
Subproblem: Reporting all intersection points, line segments
Related: Reporting all intersection points, convex polygons, Reporting all intersection points, general polygons, Counting number of intersection points, line segments
Parameters
n: number of line segments
k: number of points of intersection
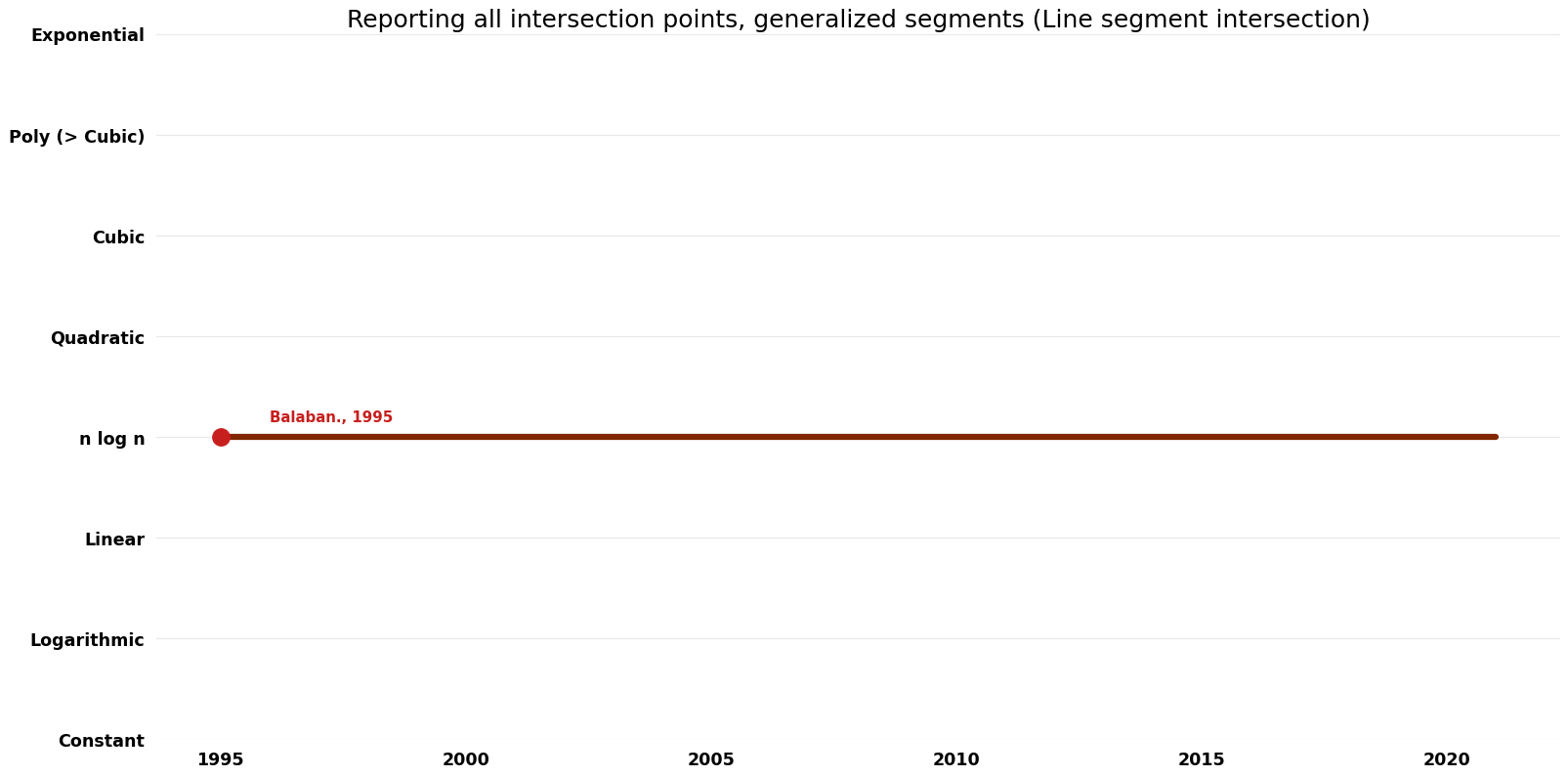
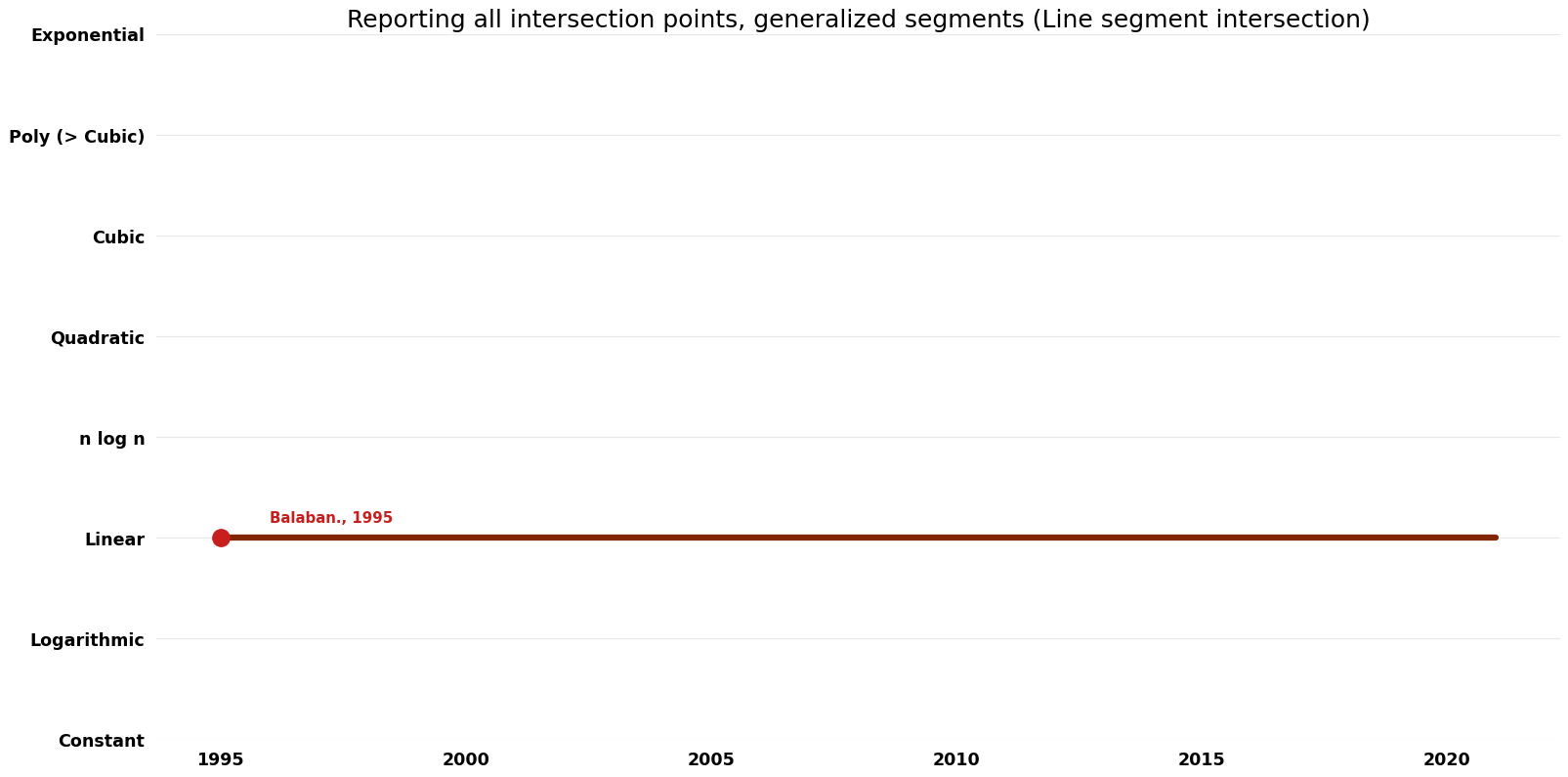
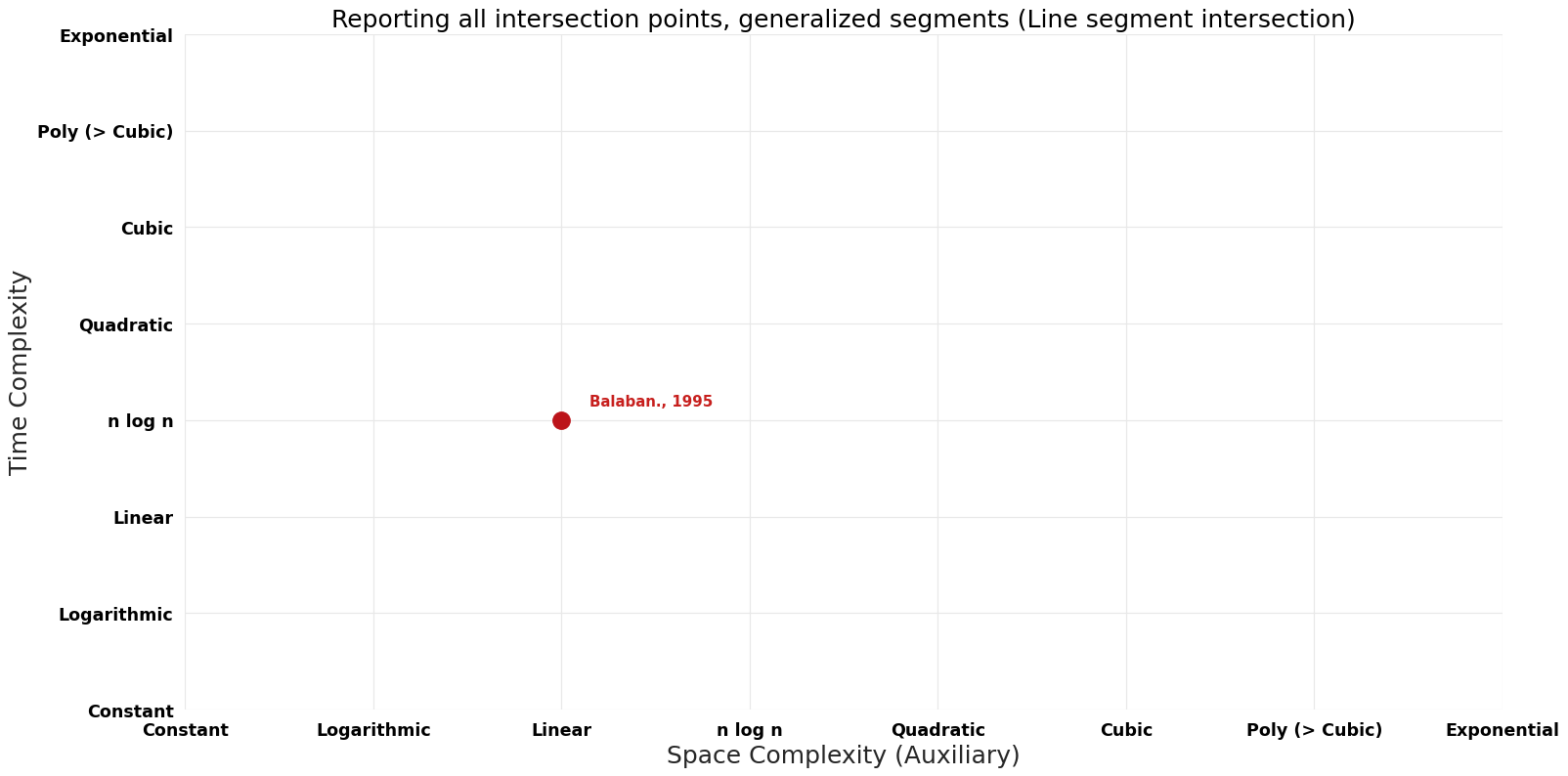
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Jean-Daniel Boissonnat and Franco P. Preparata. | 1997 | $O( n log n + k log n)$ | $O(n)$ | Exact | Deterministic | Time & Space |
| Balaban. | 1995 | $O( nlog n + k )$ | $O(n)$ | Exact | Deterministic | Time & Space |
| Boissonnat; Snoeyink | 1999 | $O( nlog n + k )$ | $O(n)$ | Exact | Deterministic | Time & Space |
Time Complexity graph
Space Complexity graph
Pareto Decades graph
