Reporting all intersection points, line segments (Line segment intersection)
Jump to navigation
Jump to search
Description
The line segment intersection problem supplies a list of line segments in the Euclidean plane and asks about the points where they intersect (cross), if any. In this case, we wish to report all points of intersection.
Related Problems
Generalizations: Reporting all intersection points, generalized segments
Subproblem: Counting number of intersection points, line segments
Related: Reporting all intersection points, convex polygons, Reporting all intersection points, general polygons
Parameters
$n$: number of line segments
$k$: number of points of intersection
Table of Algorithms
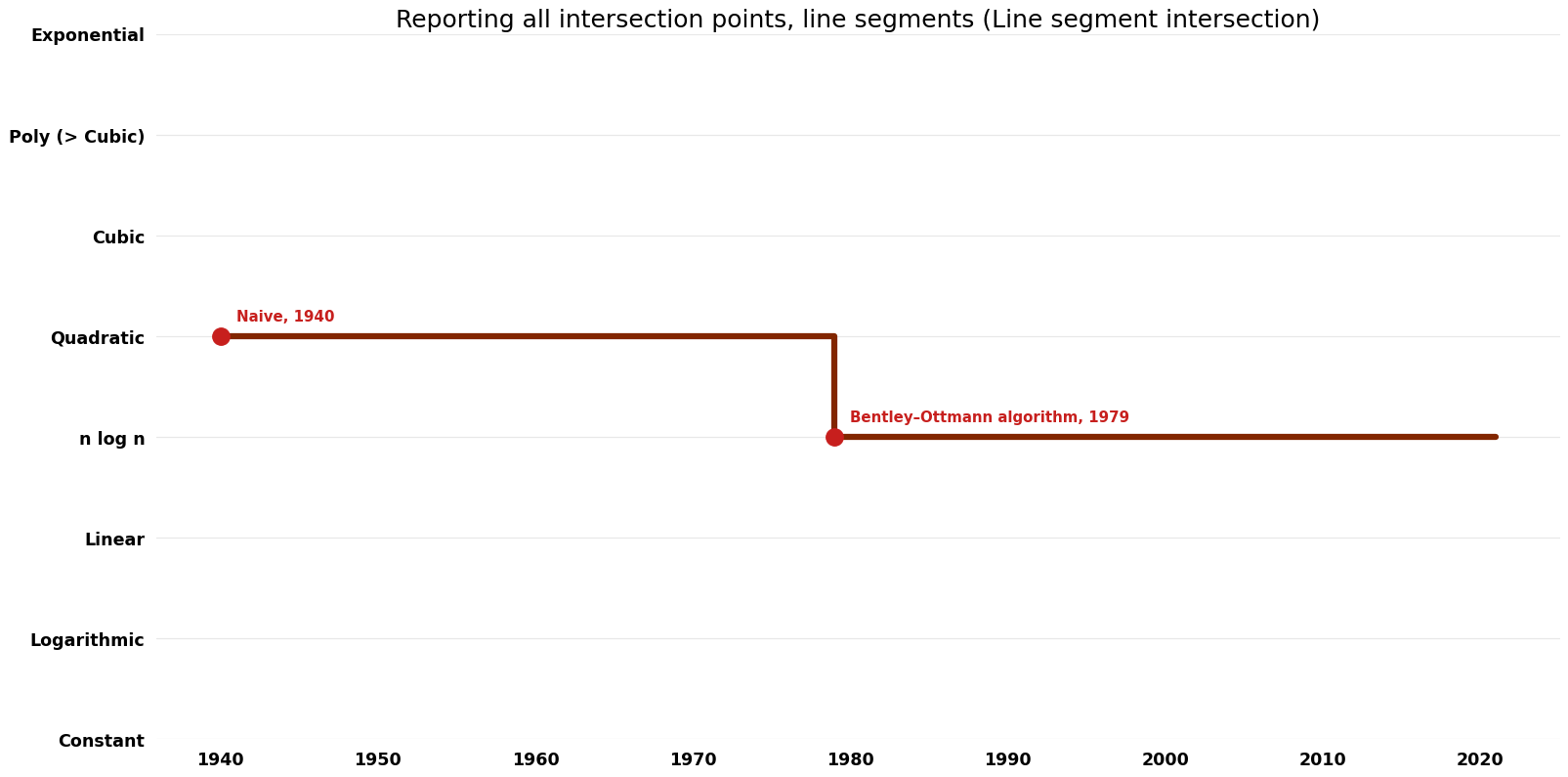
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Naive | 1940 | $O(n^{2})$ | $O({1})$ | Exact | Deterministic | |
| Bentley–Ottmann algorithm | 1979 | $O( n \log n + k \log n)$ | $O(n)$ | Exact | Deterministic | Time & Space |
| Chazelle & Edelsbrunner | 1992 | $O( n \log n + k )$ | $O(n+k)$ total? | Exact | Deterministic | Time & Space |
| CHAZELLE | 1986 | $O( n*log^{2}(n)/(log log n) + k)$ | $O(n+k)$ total (and possibly auxiliary as well?) | Exact | Deterministic | Time & Space |
| Goodrich | 1989 | $O(\log^{2}(n))$ | $O(n+k)$ total? | Exact | Parallel | Time |