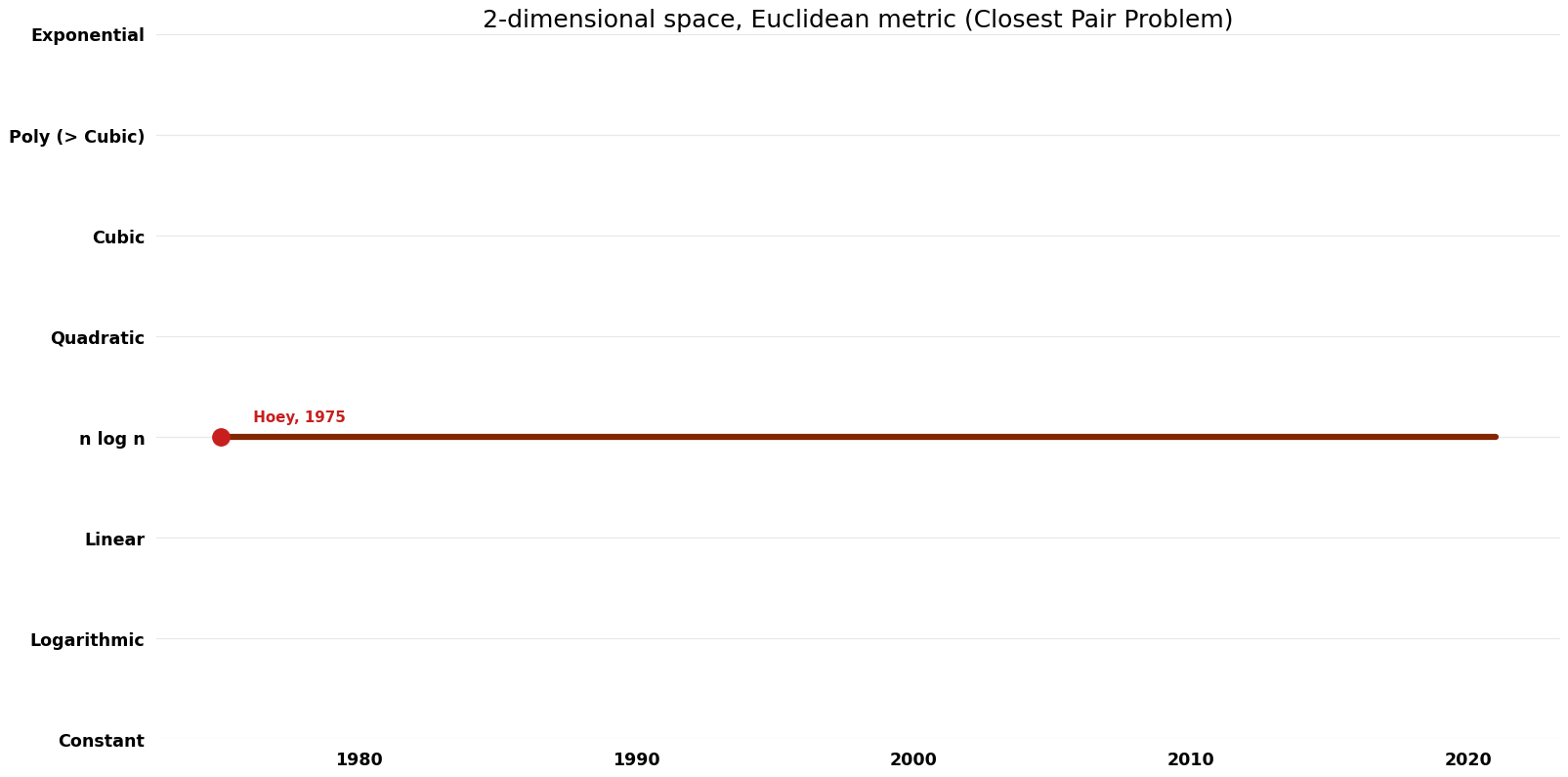
2-dimensional space, Euclidean metric (Closest Pair Problem)
Jump to navigation
Jump to search
Description
Given $n$ points in 2-dimensional space equipped with the Eucildean metric, find a pair of points with the smallest distance between them.
Related Problems
Related: k-dimensional space, $l_m$ (or $l_\infty$) norm, 2-dimensional space, $l_m$ (or $l_\infty$) norm, 2-dimensional array representation
Parameters
$n$: number of points
$k$: dimension of space
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Khuller; Matias | 1995 | $O(n)$ | $O(n)$, not sure if this is auxiliary | Exact | Randomized | Time & Space |
| Shamos; Hoey | 1975 | $O(n \log n)$ | $O(n)$ | Exact | Deterministic | Time |