Hyperbolic Spline Interpolation (Hyperbolic Spline Interpolation)
Jump to navigation
Jump to search
Description
The problem of restoring complex curves and surfaces from discrete data so that their shape is preserved is called isogeometric interpolation. A very popular tool for solving this problem are hyperbolic splines in tension, which were introduced in 1966 by Schweikert. These splines have smoothness sufficient for many applications; combined with algorithms for the automatic selection of the tension parameters, they adapt well to the given data. Unfortunately, the evaluation of hyperbolic splines is a very difficult problem because of roundoff errors (for small values of the tension parameters) and overflows (for large values of these parameters).�
Parameters
$n$: number of points
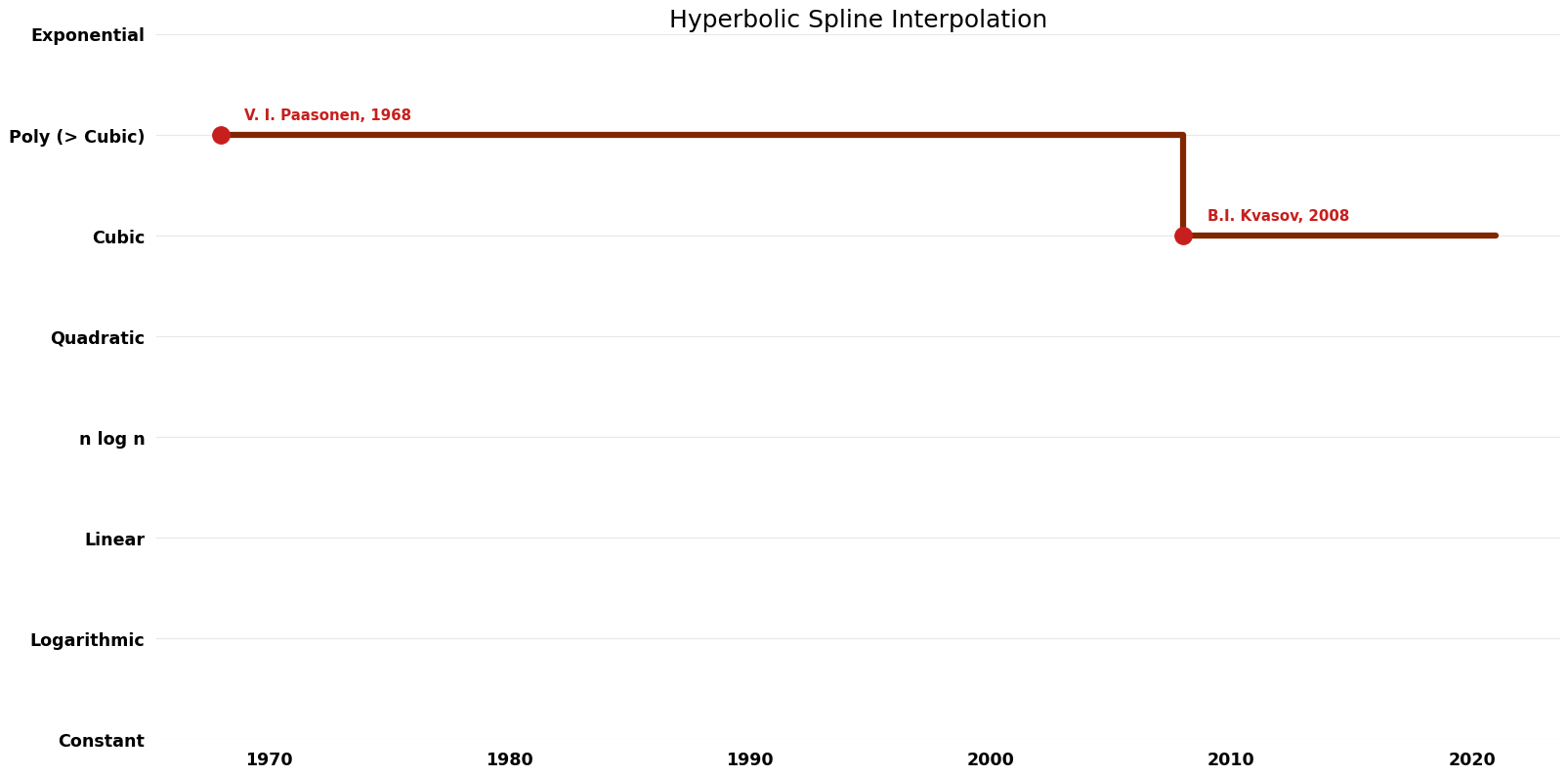
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| B.I. Kvasov | 2008 | $O(n^{3} \log^{2}K)$ | $O(n)$? | Exact | Deterministic | Time |
| V. A. Lyul’ka and A. V. Romanenko | 1994 | $O(n^{5})$ | Exact | Deterministic | Time | |
| V. A. Lyul’ka and I. E. Mikhailov | 2003 | $O(n^{4})$ | Exact | Deterministic | Time | |
| V. I. Paasonen | 1968 | $O(n^{5} \log K)$ | Exact | Deterministic | ||
| P. Costantini, B. I. Kvasov, and C. Manni | 1999 | $O(n^{5} \log K)$ | $O(n)$? | Exact | Deterministic | Time |
| B. I. Kvasov | 2000 | $O(n^{4})$ | $O(n)$?? | Exact | Deterministic | Time |