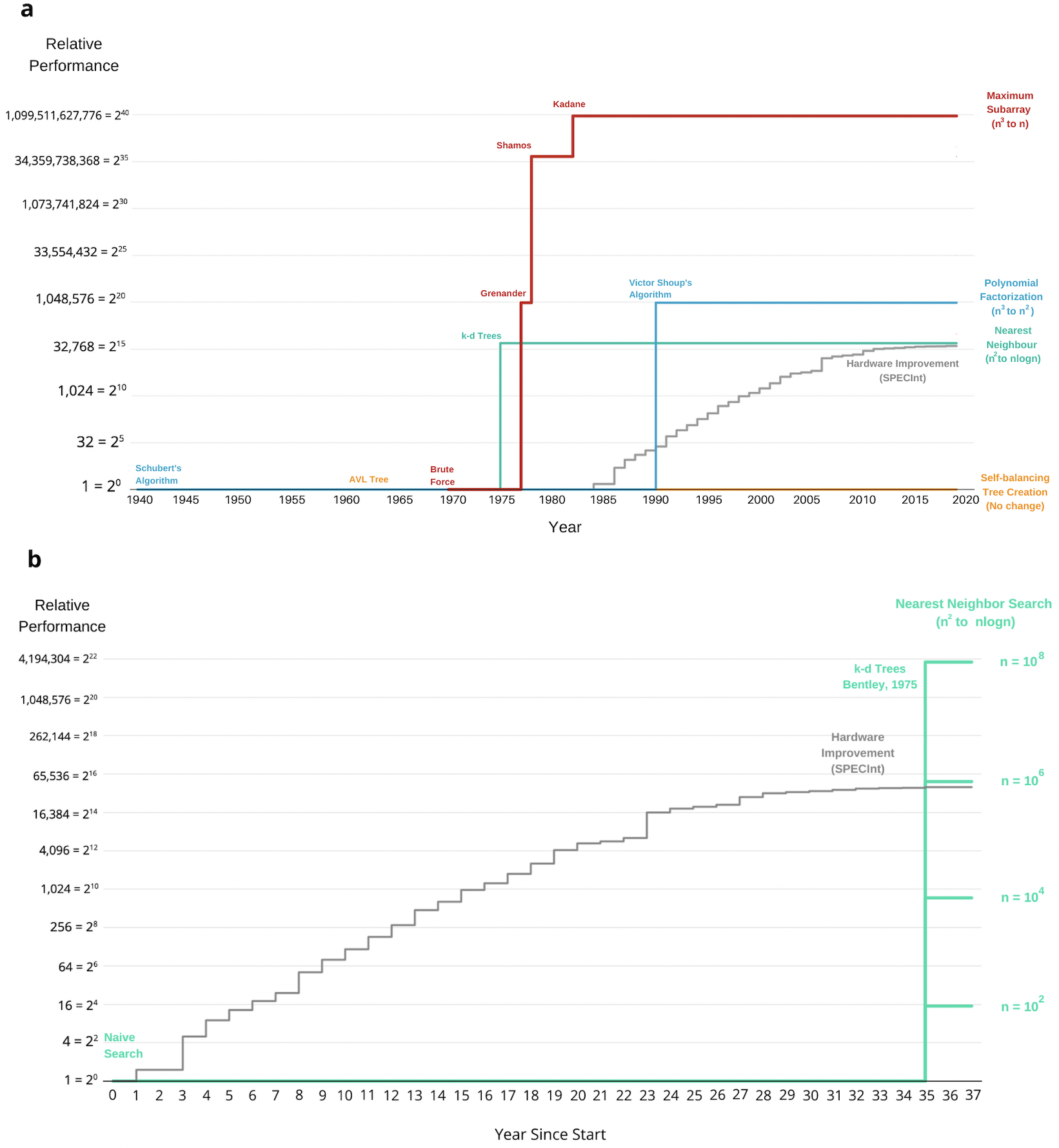
Improvement Rankings
This analysis shows the progress over time for four different algorithm families, each shown in one color. In each case, performance is normalized to $1$ for the first algorithm in that family. Whenever an algorithm is discovered with better asymptotic complexity, it is represented by a vertical step up. For example, Grenander's algorithm for the maximum subarray problem, which is used in genetics (and elsewhere), is an improvement of 1 million times over the brute force algorithm.
To provide a reference point for the magnitude of these rates, the figure also shows the SPECInt benchmark progress time series compiled in Computer Architecture books, which encapsulates the effects that Moore's Law, Dennard scaling and other hardware improvements had on-chip performance. Throughout this article, we use this measure as the hardware progress baseline. The figure shows that, for problem sizes of n=1 million, some algorithms, such as maximum subarray, have improved much more rapidly than hardware / Moore's Law, while others like Self-balancing Tree Creation have not. The orders of magnitude of variation shown in just these 4 of our 113 families make it clear why overall algorithm improvement estimates based on small numbers of case studies are unlikely to be representative of the field as a whole.
An important contrast between algorithm and hardware improvement comes in the predictability of improvements. Whereas Moore's Law led to hardware improvements happening smoothly over time, the figure shows that algorithms experience large, but infrequent improvements.