Integer Factoring (Integer Factoring)
Jump to navigation
Jump to search
Description
Given an $n$-bit integer $N$, find a non-trivial factorization $N=pq$ (where $p, q>1$ are integers) or return that $N$ is prime. For "first category" algorithms, the running time depends on the size of smallest prime factor.
Related Problems
Related: Smallest Factor
Parameters
$n$: number of bits in the integer
$B$: bound parameter (if needed)
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
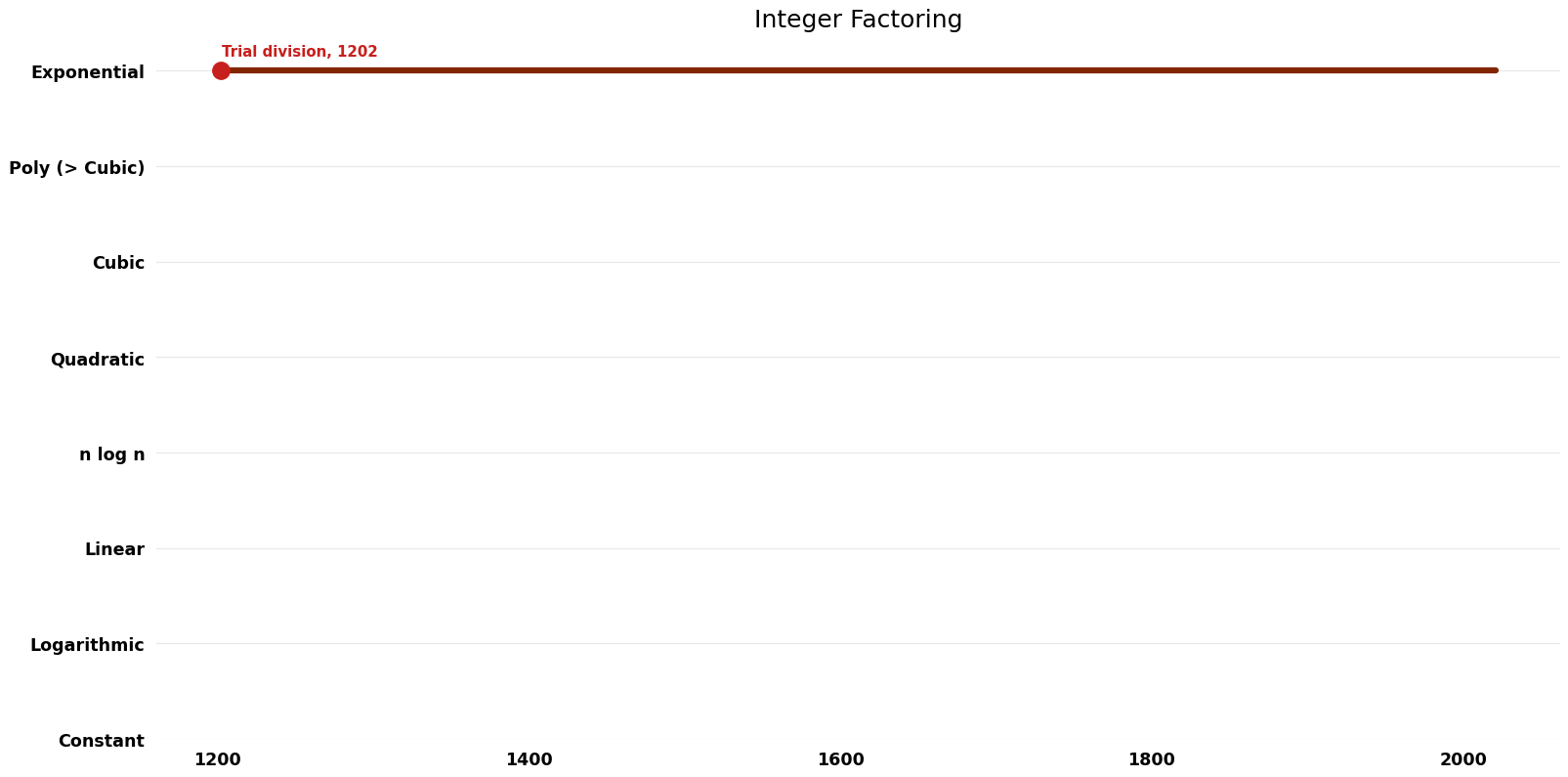
| Trial division | 1202 | $O({2}^{n/2})$ | $O(n)$ | Exact | Deterministic | |
| Wheel factorization | 1940 | $O({2}^{n/2})$ | $O(n)$ | Exact | Deterministic | |
| Pollard's rho algorithm | 1975 | - | $O(n)$ | Exact | Deterministic | Time |
| Pollard's p − 1 algorithm | 1974 | $O(B*log B*log^{2}(n)$)? | $O(n+B)$ | Exact | Deterministic | Time |
| Williams' p + 1 algorithm | 1982 | $O({2}^n)$ | $O(n)$? | Exact | Deterministic | Time |
| Lenstra elliptic curve factorization | 1987 | $O(e^{(\sqrt(({1}+o({1}))n*log n))})$ | $O(n)$? | Exact | Deterministic | Time |
| Fermat's factorization method | 1894 | $O({2}^n)$ | $O(n)$? | Exact | Deterministic | Time |
| Euler's factorization method | 1940 | $O({2}^{(n/{2})})$ | $O(n)$ | Exact | Deterministic | |
| Dixon's algorithm | 1981 | $O(e^{({2} \sqrt({2}) \sqrt(n*logn))}){4} | $O(n+(B/logB)$^{2})? | Exact | Deterministic | Time |
| Continued fraction factorization (CFRAC) | 1931 | $O(e^{\sqrt({2}n*logn)})$ | $O(n+(B/logB)$^{2})? | Exact | Deterministic | Time |
| Quadratic sieve | 1981 | - | $O(n+(B/logB)$^{2})? | Exact | Deterministic | Time |
| Rational sieve | 1993 | $O(e^{sqrt(({2}+o({1})$)n*logn)}) | $O(n+(B/logB)$^{2})? | Exact | Parallel | Time |
| Shanks's square forms factorization (SQUFOF) | 2007 | $O({2}^{n/4})$ | $O(n)$? | Exact | Deterministic | Time |
| Special number field sieve | 1940 | $O(exp(({1}+o({1})$)({32}n/{9})^{({1}/{3})}(log n)^{({2}/{3})}) heuristically? | $O(n^{2/3})$ | Exact | Deterministic | Space |
| General number field sieve | 1996 | $O(exp(({1}+o({1})$)({64}n/{9})^{({1}/{3})}(log n)^{({2}/{3})}) heuristically? | $O(n^{2/3})$ | Exact | Deterministic | Time & Space |
| Shor's algorithm Quantum Implementation | 1994 | $O(n)$ | $O(n)$ | Exact | Quantum | Time & Space |