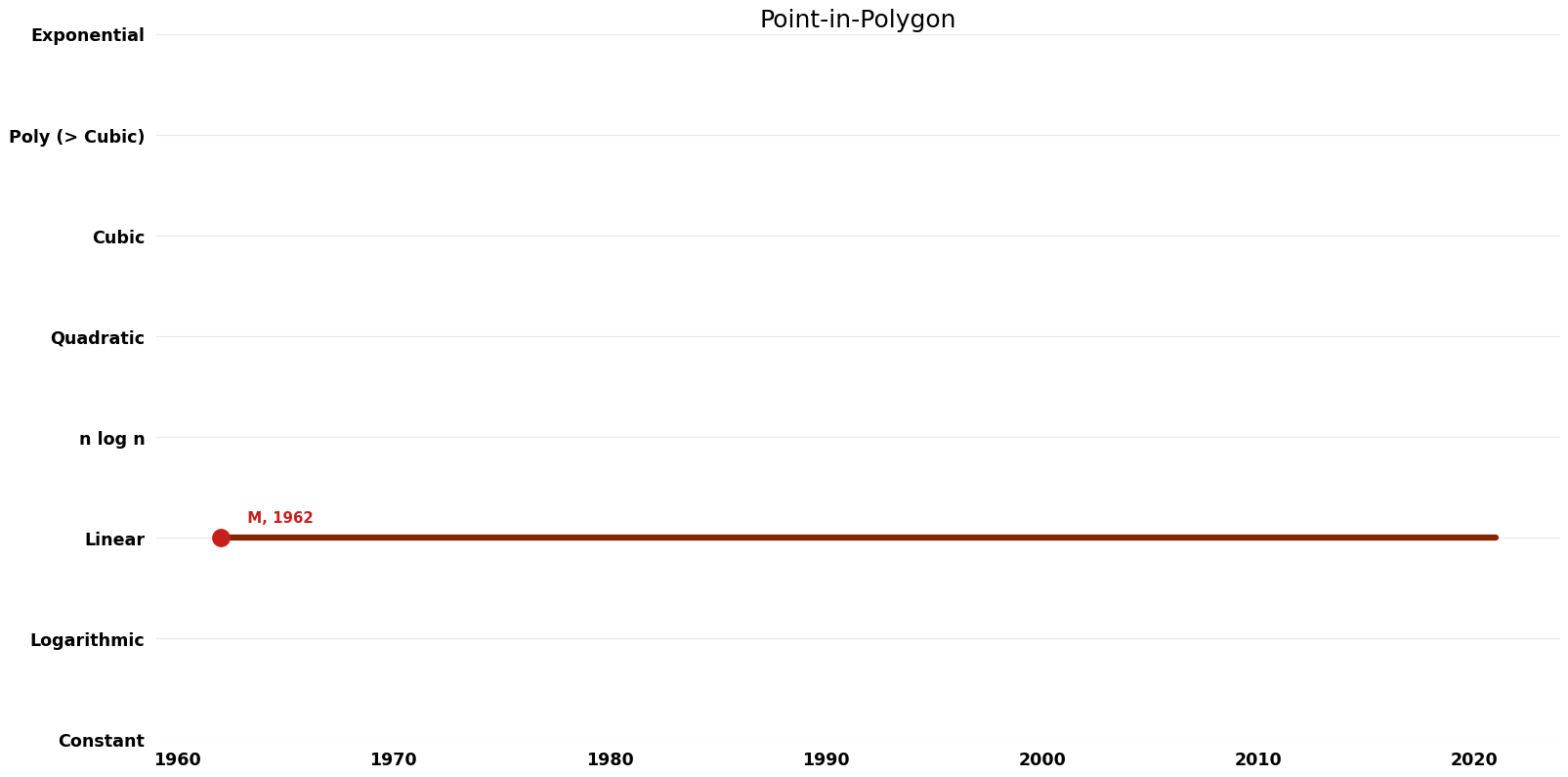
Point-in-Polygon (Point-in-Polygon)
Jump to navigation
Jump to search
Description
With a given polygon $P$ and an arbitrary point $q$, determine whether point $q$ is enclosed by the edges of the polygon.
Parameters
$n$: number of edges of polygon
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Ray casting algorithm Shimrat; M | 1962 | $O(n)$ | $O({1})$ | Exact | Deterministic | Time |
| Nordbeck and Rystedt (Grid Method) | 1967 | $O(n)$ | $O(n)$ | Exact | Deterministic | Time & Space |
| Salomon (Swath Method) | 1978 | $O(n\log n)$ | $O(n^{2})$ | Exact | Deterministic | Time & Space |
| Nordbeck and Rystedt (Sum of area) | 1967 | $O(n)$ | $O({1})$ | Exact | Deterministic | Time |
| Preparata and Shamos (Wedge) | 1985 | $O(n)$ | $O(n)$ | Exact | Deterministic | Time & Space |
| Saalfeld (Sign of offset) | 1987 | $O(n)$ | $O({1})$ | Exact | Deterministic | Time |
| Preparata and Shamos (Intersection sum of angle) | 1985 | $O(n)$ | $O({1})$ | Exact | Deterministic | Time |
| Nordbeck and Rystedt (Orientation) | 1967 | $O(n)$ | $O({1})$ | Exact | Deterministic | Time |