Positive Definite, Hermitian Matrix (Linear System)
Jump to navigation
Jump to search
Description
In this case, we restrict $A$ to be positive definite and hermitian (or symmetric, if $A$ is real-valued).
Related Problems
Generalizations: General Linear System
Related: Sparse Linear System, Non-Definite, Symmetric Matrix, Toeplitz Matrix, Vandermonde Matrix
Parameters
$n$: number of variables and number of equations
$m$: number of nonzero entries in matrix
$k$: ratio between largest and smallest eigenvalues
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
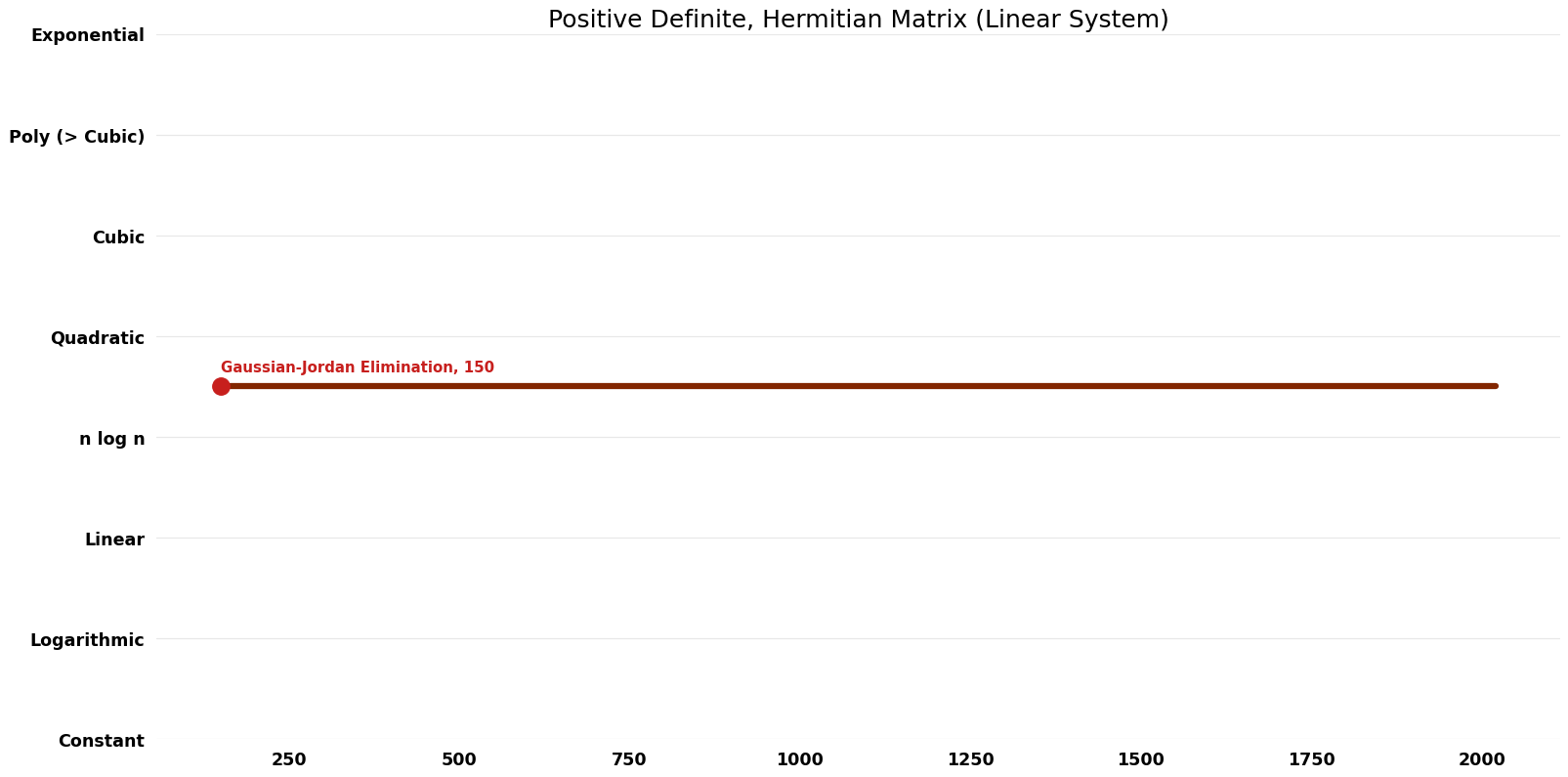
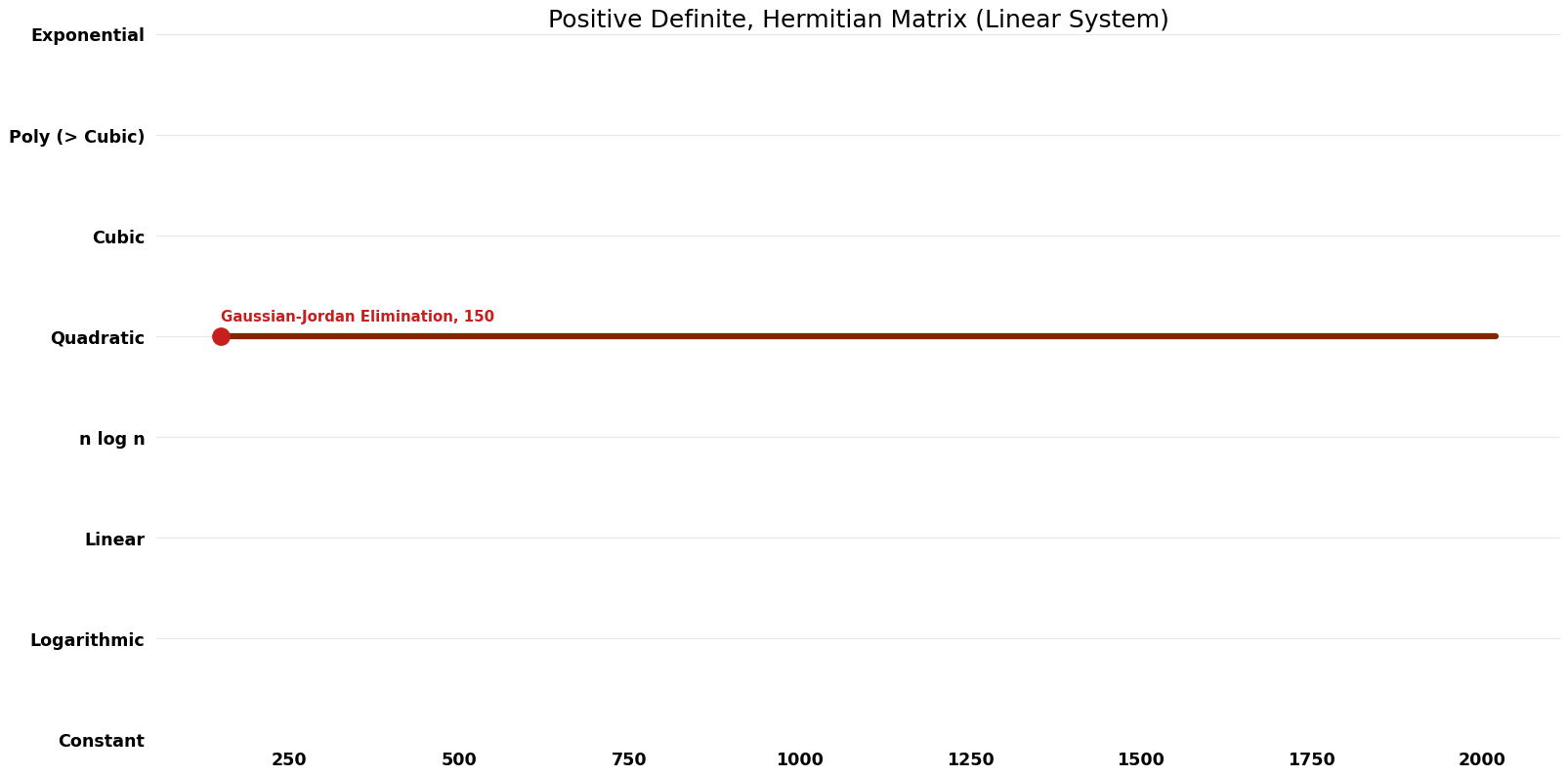
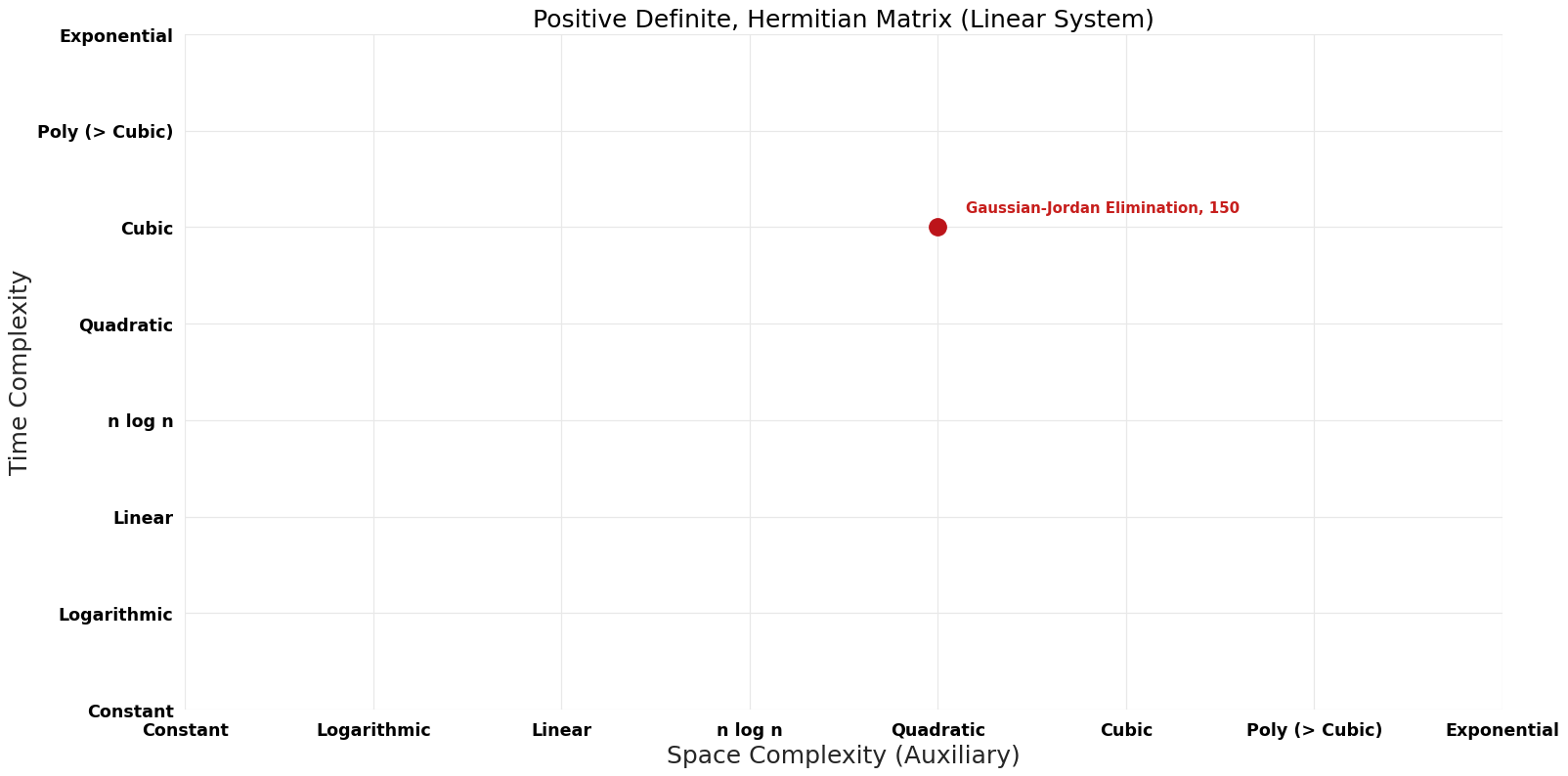
| Gaussian-Jordan Elimination | -150 | $O(n^{3})$ | $O(n^{2})$ | Exact | Deterministic | |
| Cholesky | 1940 | $O(n^{3})$ | $O(n^{2})$ | Exact | Deterministic |
Time Complexity Graph
Space Complexity Graph
Time-Space Tradeoff
