Single String Search (String Search)
Jump to navigation
Jump to search
Description
Single string search algorithms try to find a place where a string (also called a pattern) is found within a larger string or text.
Related Problems
Related: Multiple String Search
Parameters
$m$: pattern length
$n$: length of searchable text
$s$: size of the alphabet
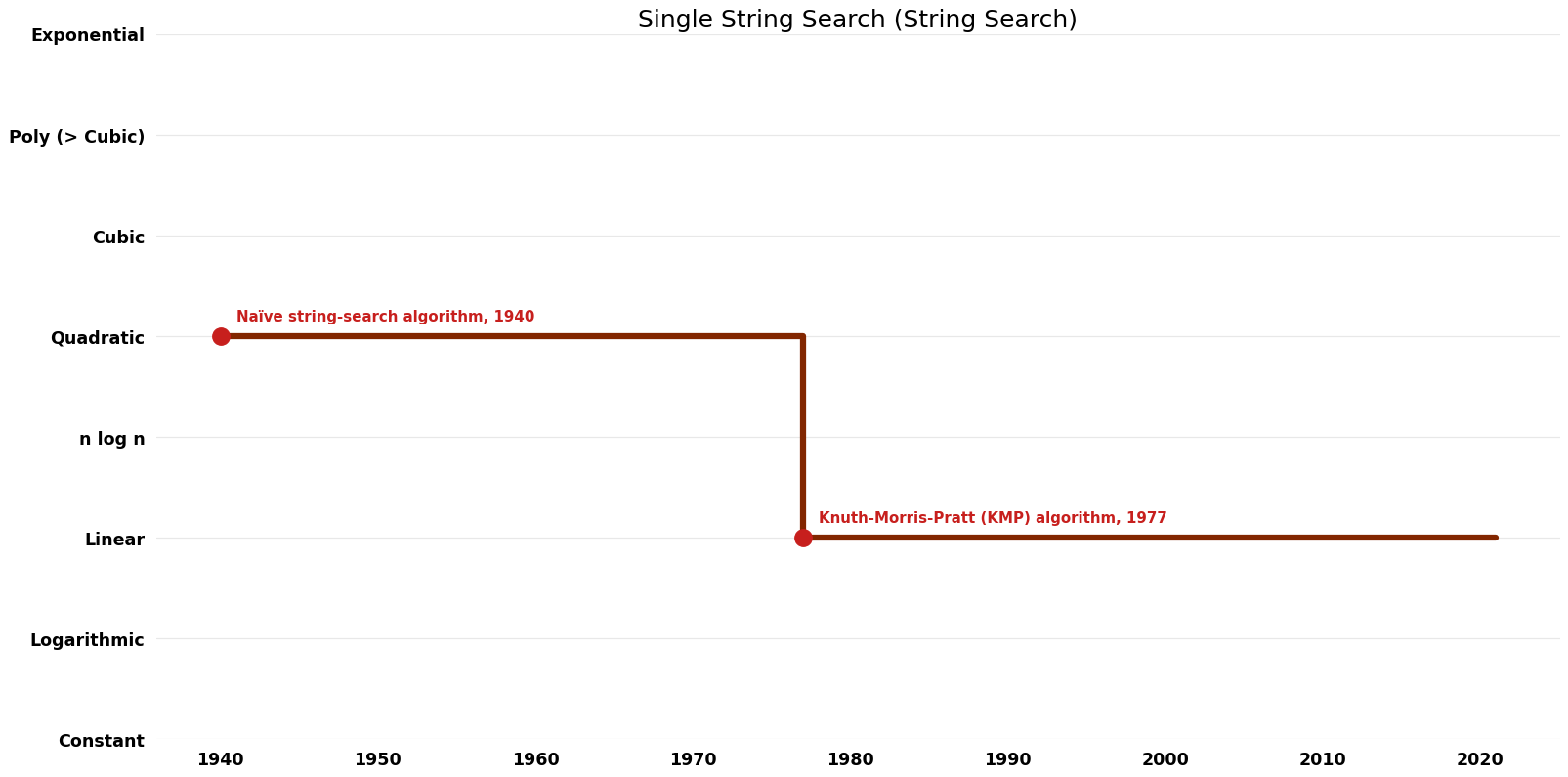
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Naïve string-search algorithm | 1940 | $O(m(n-m+{1}))$ | $O({1})$ | Exact | Deterministic | |
| Knuth-Morris-Pratt (KMP) algorithm | 1977 | $O(m+n)$ | $O(m)$ | Exact | Deterministic | Time & Space |
| Boyer-Moore (BM) algorithm | 1977 | $O(mn + s)$ | $O(s)$ | Exact | Deterministic | Time & Space |
| Rabin-Karp (RK) algorithm | 1987 | $O(mn)$ | $O({1})$ | Exact | Deterministic | Time |
| Bitap algorithm | 1964 | $O(mn)$ | $O(m)$ | Exact | Deterministic | Time |
| Tuned Boyer-Moore algorithm | 1991 | $O(mn)$ | $O(m + s)$ | Exact | Deterministic | Time & Space |
| Two-way String-Matching Algorithm | 1991 | $O(n + m)$ | $O({1})$ | Exact | Deterministic | Time & Space |
| String-Matching with Finite Automata | 1940 | $O(mn)$ | $O(m)$ | Exact | Deterministic | |
| Quick-Skip Searching | 2012 | $O(mn)$ | $O(m)$ | Exact | Deterministic | Time |
| Fast Hybrid Algorithm | 2017 | $O(n+m)$+ $O(m+s)$ | $O(m)$ | Exact | Deterministic | Time |
| Backward Non-Deterministic DAWG Matching (BNDM) | 1998 | $O(n+m)$ | $O(sm)$ | Exact | Parallel | Time & Space |
| Boyer-Moore-Horspool (BMH) | 1980 | $O(mn + s)$ | $O(s)$ | Exact | Deterministic | Time |
| Raita Algorithm | 1991 | $O(mn + s)$ | $O(s)$ | Exact | Deterministic | Time |
| BOM (Backward Oracle Matching) | 1999 | $O(m)$ + $O(mn)$ | $O(m)$ | Exact | Deterministic | Time & Space |
| Apostolico–Giancarlo Algorithm | 1986 | $O(m + s)$ + $O(n)$ | $O(m)$ | Exact | Deterministic | Time & Space |
| Wu and Manber, Fuzzy String Matching | 1992 | $O(nk \lceil m/w \rceil)$ | $O(ms + k \lceil m/w \rceil)$ | Levensthein Distance = k | Deterministic | Time & Space |