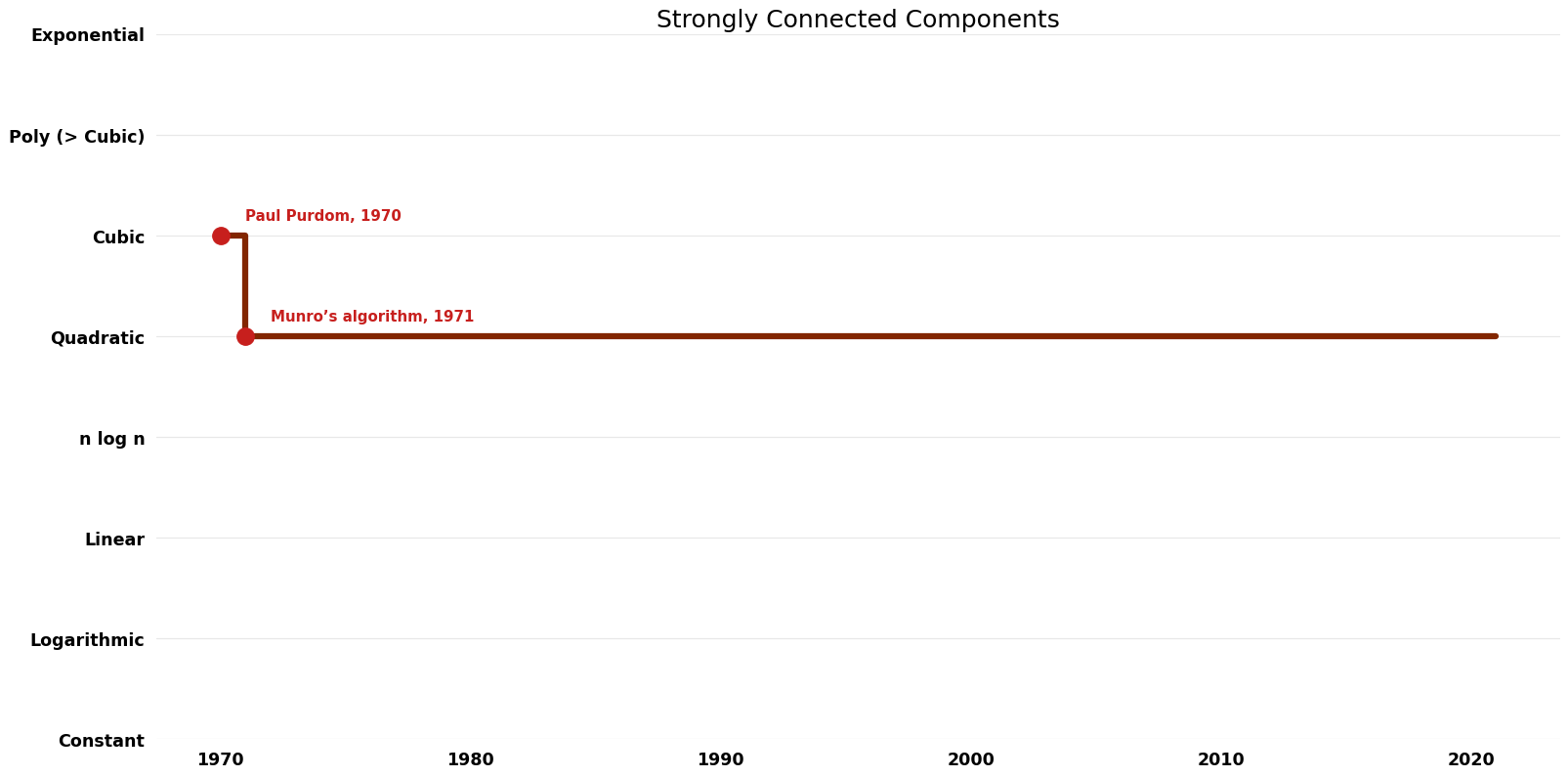
Strongly Connected Components (Strongly Connected Components)
Jump to navigation
Jump to search
Description
The strongly connected components or diconnected components of an arbitrary directed graph form a partition into subgraphs that are themselves strongly connected.
Related Problems
Related: Transitive Closure, Maximum Strongly Connected Component, Strong Connectivity (dynamic), 2 Strong Components (dynamic), Connected Subgraph
Parameters
$V$: number of vertices
$E$: number of edges
Table of Algorithms
Currently no algorithms in our database for the given problem.
Time Complexity Graph
